SOLUTION: Gabby is 1 year more than twice Larry's age. 3 years from now, Megan will be 27 less than twice Gabby's age. 4 years ago, Megan was 1 year less than 3 times Larry's age. How old wi

Algebra ->  Customizable Word Problem Solvers  -> Age -> SOLUTION: Gabby is 1 year more than twice Larry's age. 3 years from now, Megan will be 27 less than twice Gabby's age. 4 years ago, Megan was 1 year less than 3 times Larry's age. How old wi      Log On

Ad: Over 600 Algebra Word Problems at edhelper.com


    

Question 1079104: Gabby is 1 year more than twice Larry's age. 3 years from now, Megan will be 27 less than twice Gabby's age. 4 years ago, Megan was 1 year less than 3 times Larry's age. How old will Megan be 3 years from now?
I'm having trouble with the equation.
Found 3 solutions by VFBundy, josgarithmetic, MathTherapy:
Answer by VFBundy(438) About Me  (Show Source):
You can put this solution on YOUR website!
G = Gabby's age now
L = Larry's age now
M = Megan's age now

Gabby is 1 year more than twice Larry's age:
G = 2L + 1

3 years from now, Megan will be 27 less than twice Gabby's age:
M + 3 = 2(G + 3) - 27

Substitute G with 2L + 1:
M + 3 = 2((2L + 1) + 3) - 27

Simplify the above:
M + 3 = 4L - 19

Solve for L:
4L = M + 22

L = (M + 22)/4

4 years ago, Megan was 1 year less than 3 times Larry's age:
M - 4 = 3(L - 4) - 1

Simplify the above:
M - 4 = 3L - 13

Solve for M:
M = 3L - 9

Substitute L with (M + 22)/4:
M+=+3%28%28M+%2B+22%29%2F4%29+-+9

Simplify above:
M+=+%283M+%2B+66%29%2F4+-+9

Solve for M:
M+=+%283M+%2B+66%29%2F4+-+36%2F4

M+=+%283M+%2B+66+-+36%29%2F4

M+=+%283M+%2B+30%29%2F4

4M = 3M + 30

M = 30

M = Megan's age now = 30

How old will Megan be 3 years from now?

M + 3 = 30 + 3 = 33

Megan will be 33 three years from now.

---------------------------------------------------
Just for kicks, their ages now:
Megan = 30
Larry = 13
Gabby = 27

Answer by josgarithmetic(39618) About Me  (Show Source):
You can put this solution on YOUR website!
G, Gabby
L, Larry
M, Megan

Literal translation of the description:
system%28G=2L%2B1%2C+M%2B3=2%28G%2B3%29-27%2CM-4=3%28L-4%29-1%29


Simplifications:
system%28G=2L%2B1%2CM%2B3=2G%2B6-27%2CM-4=3L-12-1%29

system%28G=2L%2B1%2CM-2G=-24%2CM-3L=-9%29

system%28G=2L%2B1%2C2G-M=24%2C3L-M=9%29
Now solve this system.

Answer by MathTherapy(10552) About Me  (Show Source):
You can put this solution on YOUR website!

Gabby is 1 year more than twice Larry's age. 3 years from now, Megan will be 27 less than twice Gabby's age. 4 years ago, Megan was 1 year less than 3 times Larry's age. How old will Megan be 3 years from now?
I'm having trouble with the equation. 
Let Megan's and Larry's ages be M, and L, respectively

Then Gabby's = 2L + 1

Also, M + 3 = 2(2L + 1 + 3) - 27_____4L = M + 22_____ 

And, M - 4 = 3(L - 4) - 1_____3L = M + 9_____matrix%281%2C7%2C+L%2C+%22=%22%2C+%28M+%2B+9%29%2F3%2C+or%2C+L%2C+%22=%22%2C+M%2F3+%2B+3%29

WIth L being 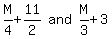matrix%281%2C3%2C+M%2F4+%2B+11%2F2%2C+and%2C+M%2F3+%2B+3%29, we can say that: matrix%281%2C3%2C+M%2F4+%2B+11%2F2%2C+%22=%22%2C+M%2F3+%2B+3%29

3M + 66 = 4M + 36 ------ Multiplying by LCD, 12

3M - 4M = 36 - 66

- M = - 30

Megan's age, or matrix%281%2C5%2C+M%2C+%22=%22%2C+%28-+30%29%2F%28-+1%29%2C+%22=%22%2C+30%29

In 3 years' time, Megan will be: highlight_green%28matrix%281%2C4%2C+30+%2B+3%2C+%22=%22%2C+33%2C+years-old%29%29