Question 1063777: After death of Diophantus (about 290 A.D.) a famous mathematician, someone described his life as a puzzle.
He was a boy for 1/6 of his life. After 1/12 more, he acquired a beard, after another 1/7, he married. 5th year after his marriage, his son was born. The son lived half as many as his father. Diophantus died 4 years after his son. How old was Diophantus when he died?
Answer by ikleyn(52786)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
After death of Diophantus (about 290 A.D.) a famous mathematician, someone described his life as a puzzle.
He was a boy for 1/6 of his life. After 1/12 more, he acquired a beard, after another 1/7, he married. 5th year after his marriage,
his son was born. The son lived half as many as his father. Diophantus died 4 years after his son. How old was Diophantus when he died?
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
Answer. D. was 84 years old when he died.
Solution
It is not difficult problem.
Moving along of his timescale, we get the equation
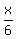 + + 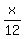 + +  + 5 + + 5 +  + 4 = x,
Where "x" is an unknown D.'s age when he died.
Multiply both sides by the common denominator, which is 84 = 12*7.
Simplify and solve for "x". You will get x = 84. + 4 = x,
Where "x" is an unknown D.'s age when he died.
Multiply both sides by the common denominator, which is 84 = 12*7.
Simplify and solve for "x". You will get x = 84.
Solved.
CHECK. Quotation from the source http://www.storyofmathematics.com/hellenistic_diophantus.html
One of the problems in a later 5th Century Greek anthology of number games is sometimes considered to be Diophantus’ epitaph:
“Here lies Diophantus.
God gave him his boyhood one-sixth of his life;
One twelfth more as youth while whiskers grew rife;
And then yet one-seventh ‘ere marriage begun.
In five years there came a bouncing new son;
Alas, the dear child of master and sage,
After attaining half the measure of his father's life, chill fate took him.
After consoling his fate by the science of numbers for four years, he ended his life.”
The puzzle implies that Diophantus lived to be about 84 years old (although its biographical accuracy is uncertain).
End of checking
CONFIRMATION. This article of Wikipedia https://en.wikipedia.org/wiki/Diophantus
https://en.wikipedia.org/wiki/Diophantus
|
|
|