Question 1061388: Laura is four years less than twice her son's age. The sum of their ages is 119. How old is Laura? How old is her son?
Found 3 solutions by ikleyn, HelpfulBro, MathTherapy:
Answer by ikleyn(52781)   (Show Source):
You can put this solution on YOUR website! .
Laura is four years less than twice her son's age. The sum of their ages is 119. How old is Laura? How old is her son?
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
L = 2S - 4, (1)
L + S = 119. (2)
From (1), substitute L = 2S - 4 into (2), replacing L. You will get
(2S-4) + S = 119.
3S = 119 + 4 = 123.
S = 41. (son)
L = 2*41 - 4 = 78. (Lora)
Answer by HelpfulBro(2)  (Show Source):
You can put this solution on YOUR website! We give representations:
let l be the age of Laura
let s be the age of Laura's son
According to the problem, Laura is four years less than twice her son's age
we write that as l = 2*s - 4 (we let this be equation 1)
It also says there that The sum of their ages is 119:
l + s = 119 (we let this be equation 2)
What we do now is to use equation one in equation two (substitution)
l + s = 119
(2*s - 4) + s= 119
3*s = 119 + 4
3*s = 123
s = 41
So, the son's age is 41. Now we solve for Laura's age using equation 1
l = 2*s - 4
l = 2*41 - 4
l = 82 - 4
l = 78
Laura's age is 78.
To check if we got it right,
l+s = 119
41 + 78 = 119
119 = 119
Answer by MathTherapy(10552)  (Show Source):
You can put this solution on YOUR website!
Laura is four years less than twice her son's age. The sum of their ages is 119. How old is Laura? How old is her son?
Let son's age, be S
Then Laura's age is: 2S - 4
We then get the following SUM-OF-AGES equation: S + 2S - 4 = 119
3S = 119 + 4
3S = 123
S, or son is: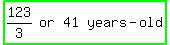 
|
|
|
