Question 1042192: Andrew has two children, David and Helen. The sum of their three ages is 49. Davidís age is three times that of Helen. In 5 years time, Andrewís age will be three times Davidís age. What is the product of their ages now?
Found 3 solutions by josgarithmetic, Theo, MathTherapy:
Answer by josgarithmetic(39617)   (Show Source): (Show Source):
You can put this solution on YOUR website! d and h; and y for Andrew's age;

Assumption used here was "The sum of ALL OF THEIR ages is 49".
Solve the system for d, h, and y, and then find 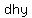 . .
Answer by Theo(13342)   (Show Source): (Show Source):
You can put this solution on YOUR website! you can solve this in several ways.
i'll show you two.
the first way is by looking at this as three equations that need to be solved simultaneously through the elimination method so you can get a solution that is common to all three.
your variables will be:
a = andrew's age today.
d = david's age today.
h = helen's age today.
your first equation is a + d + h = 49
this equations says that the sum of their ages is 49.
your second equation is d = 3h
this equation says that david's age is 3 times that of helen's age.
your third equation is a + 5 = 3 * (d + 5)
this equation says that, in 5 years, andrew will be 3 times as old as david will be then.
andrew's age today is a.
his age in 5 years is a + 5.
david's age today is d.
his age in 5 years is d + 5.
your three equations are:
a + d + h = 49
d = 3h
a + 5 = 3 * (d + 5)
rearrange the equations so that all the variable terms are on the left and all the constant terms are on the right.
your first equations stays the same.
your second equation starts as d = 3h.
subtract 3h from both sides to get d - 3h = 0.
your third equation starts as a + 5 = 3 * (d + 5)
simplify to get a + 5 = 3 * d + 3 * 5
simplify further to get a + 5 = 3 * d + 15
subtract 5 from both sides and subtract 3 * d from both sides to get a - 3 * d = 15 - 5
simplify to get a - 3d = 10
your 3 equations are now:
a + d + h = 49 (equation 1)
d - 3h = 0 (equation 2)
a - 3d = 10 (equation 3)
subtract equation 2 from equation 1 to get:
(a + d + h) - (d - 3h) = 49 - 0
simplify to get:
a + d + h - d + 3h = 49
combine like terms to get:
a + 4h = 49 (equation 4)
you eliminated d from equations 1 and 2 by subtracting equation 2 from equation 1.
now you want to eliminate d from equations 2 and 3.
equations 2 and 3 are:
d - 3h = 0 (equation 2)
a - 3d = 10 (equation 3)
multiply both sides of equation 2 by 3 to get:
3d - 9h = 0 (equation 2a)
a - 3d = 10 (equation 3)
add equations 2a and 3 together to get:
(3d - 9h) + (a - 3d) = 0 + 10
simplify to get:
3d - 9h + a - 3d = 10
combine like terms to get:
-9h + a = 10 (equation 5)
you have two equations that only have a and h in them.
they are:
a + 4h = 49 (equation 4)
-9h + a = 10 (equation 5)
you can eliminate the variable a by subtracting equation 5 from equation 4.
subtract equation 5 from equation 4 to get:
(a + 4h) - (-9h + a) = 49 - 10
simplify to get:
a + 4h + 9h - a = 39
combine like terms to get:
13h = 39
divide both sides of this equation by 13 to get:
h = 3
you now know that the value of h is equal to 3.
since d = 3h, then the value of d has to be 9.
since a + d + h = 49, then the value of a has to be 37.
you have your solution.
andrew is 37 years old.
david is 9 years old.
helen is 3 years old.
all the requirements of the problem are satisfied.
the sum of their ages is 49.
david is 3 times as old as helen.
this is because 9 is equal to 3 * 3.
in 5 years, andrew will be 3 times as old as david.
this is because 37 + 5 = 42 and 9 + 4 = 14 and 42 = 3 * 14.
the above is the more formal way of solving this problem.
the same method will be used for more complex problems as you get into solving simultaneous equations using matrices of coefficients and constants.
you can also solve it logically as follows:
start with your 3 original equations as before.
they are:
a + d + h = 49 (first equation)
d = 3h (second equation)
a + 5 = 3 * (d + 5) (third equation)
since d = 3h, replace d in the first equation with 3h to get:
first equation becomes a + 3h + h = 49
combine like terms to get:
first equation now equals a + 4h = 49
if you can get a in terms of h, then you can solve for h.
your third equation is a + 5 = 3 * (d + 5)
simplify this to get a + 5 = 3 * d + 15
subtract 5 from both sides of this equation to get a = 3 * d + 10
since you already know that d = 3h, you can replace d with 3h to get:
a = 3 * 3h + 10
simplify to get:
a = 9h + 10
in your first equation of a + 4h = 49, replace a with (9h + 10) to get:
(9h + 10) + 4h = 49
simplify to get:
9h + 10 + 4h = 49
combine like terms to get 13h + 10 = 49
subtract 10 from both sides to get 13h = 39
solve for h to get h = 3.
once you know h = 3, then d = 3h becomes 9 and a + d + h = 49 gets you a = 37.
same answer as before, only done through more informal type logic rather than a systematic analysis of solving three equations simultaneously using the elimination method.
this last method would fall more in line with solving three equations simultaneously through the substitution method.
Answer by MathTherapy(10552)   (Show Source): (Show Source):
You can put this solution on YOUR website!
Andrew has two children, David and Helen. The sum of their three ages is 49. Davidís age is three times that of Helen. In 5 years time, Andrewís age will be three times Davidís age. What is the product of their ages now?
Let Helen's age be H, and Andrew's, A
Then David's is: 3H
We also get: A + 5 = 3(3H + 5)
A + 5 = 9H + 15
A = 9H + 10
Since their ages sum to 49, then we get: H + 3H + 9H + 10 = 49
13H = 49 - 10
13H = 39
H, or Helen's age = 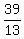 , or 3 , or 3
David's age: 3(3), or 9
Andrew's age: 49 - (3 + 9), or 49 - 12, or 37
Product of their ages: 3(9)(37). Do you think you can find this?
|
|
|