Question 1024237: A Canoe traveled Downstream with the current and went a distance of 15 miles in three hours. On the return trip, the canoe traveled Upstream against the current. It took 5 hours to make the return trip. Find the rate of the current.
Please show the work
Answer by ikleyn(52800)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
A Canoe traveled Downstream with the current and went a distance of 15 miles in three hours.
On the return trip, the canoe traveled Upstream against the current. It took 5 hours to make the return trip. Find the rate of the current.
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
Let u = the canoe speed in still water (the speed relative to water), in mph.
v = the speed of the current.
When canoe travels downstream, its speed relative to the bank of the river is the sum u + v, and it is equal to
u + v =  (speed = (speed = 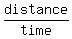 ).
When canoe travels upstream, its speed relative to the bank of the river is the difference u - v, and it is equal to
u - v = ).
When canoe travels upstream, its speed relative to the bank of the river is the difference u - v, and it is equal to
u - v = 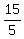 (again, speed = (again, speed = 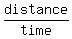 ).
Rewrite these equations with calculated right sides:
u + v = 5, (1)
u - v = 3. (2)
Now add equations (1) and (2) (both sides). You will get
2u = 5 + 3 = 8.
Hence, u = ).
Rewrite these equations with calculated right sides:
u + v = 5, (1)
u - v = 3. (2)
Now add equations (1) and (2) (both sides). You will get
2u = 5 + 3 = 8.
Hence, u = 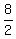 = 4 mph. It is the canoe speed in still water.
Next, from (1) v = 5 - u = 5 - 4 = 1 mph. It is the current speed. = 4 mph. It is the canoe speed in still water.
Next, from (1) v = 5 - u = 5 - 4 = 1 mph. It is the current speed.
|
|
|