Question 1017852: The sum of the ages of Ron and Iezus is 92. In 6 years, the difference of their ages is 24. Given that Ron is older than Iezus, how old is each now?
Found 3 solutions by rothauserc, addingup, MathTherapy:
Answer by rothauserc(4718)   (Show Source): (Show Source):
You can put this solution on YOUR website! Let R be age of Ron and I be ae of Iezus, then
1) R + I = 92
2) (R+6) - (I+6) = 24
:
solve equation 1 for I
I = 92 - R
:
now substitute for I in equation 2
:
(R+6) - (92-R+6) = 24
R+6 -92+R-6 = 24
2R = 116
R = 58
I = 92 - 58 = 34
:
*********************************
Ron is 58 and Iezus is 34
*********************************
:
now check our answer by substituting for R and I in equation 2
:
(58+6) - (34+6) = 24
64 - 40 = 24
24 = 24
our answer checks :-)
Answer by addingup(3677)   (Show Source): (Show Source):
You can put this solution on YOUR website! R+I = 92 and thus R = 92-I
R+6 = I+6+24
R+6 = I+30 substitute for R:
92-I+6 = I+30
98-I = I+30
68 = 2I
34 = I So Iezus is 34 and Ron:
34+24 = 58 And:
34+58 = 92 just like the problem says.
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
NOTE: The problem is worded to confuse you: "In 6 year the difference in age is 24"
The difference in age is going to be the same throughout their lives. For example, let's say I'm 30 and you are 15. We can say I am twice your age (15*2=30) and we can say I am 15 years older than you are (15+15 = 30). In 10 years, you will be 25 and I will be 40. You are no longer half my age, in fact you seem to be catching up with me! But notice that the difference in age is still 15 (25+15= 40). Beware of this type of trap in word problems.
J
Answer by MathTherapy(10551)   (Show Source): (Show Source):
You can put this solution on YOUR website!
The sum of the ages of Ron and Iezus is 92. In 6 years, the difference of their ages is 24. Given that Ron is older than Iezus, how old is each now?
Let Ron's age be R, and Iezus', I
Then: R + I = 92 -------- eq (i)
Once their ages differ by 24, it doesn't matter which year they're in, their ages will
always differ by 24, and since Ron is older, we get: R = 24 + I --------- eq (ii)
24 + I + I = 92 --------- Substituting 24 + I for R in (i)
2I = 92 - 24
2I = 68
I, or Iezus' age = 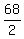 , or , or 
R = 24 + 34 --------- Substituting 34 for I in eq (ii)
R, or Ron's age = 
|
|
|