Question 1012731: 4 members of a family 10 years ago, the average age was 24 years old | 2 Children born after the family still has the same average age | Assuming that the child is under the age of 2 years, the difference | The current age of the children, find?
Found 2 solutions by Edwin McCravy, ankor@dixie-net.com:
Answer by Edwin McCravy(20059)   (Show Source): (Show Source):
You can put this solution on YOUR website!
10 years ago the father was 35, the mother was 33,
the girl was 13 and the boy was 15, their average age was
 Now, 10 years later, the father is 45, the mother is 43,
the girl is now a woman 23, the boy is now a man 25.
7 years ago the wife had a baby boy, who is now 7 years old.
1 year ago the wife had a baby girl, who is now 1 year old.
Now their average age is also:
Now, 10 years later, the father is 45, the mother is 43,
the girl is now a woman 23, the boy is now a man 25.
7 years ago the wife had a baby boy, who is now 7 years old.
1 year ago the wife had a baby girl, who is now 1 year old.
Now their average age is also:
 The average is the same, 24, and the baby is under 2 years of age.
But there are many other solutions as well.
Edwin
The average is the same, 24, and the baby is under 2 years of age.
But there are many other solutions as well.
Edwin
Answer by ankor@dixie-net.com(22740)   (Show Source): (Show Source):
You can put this solution on YOUR website! 4 members of a family 10 years ago, the average age was 24 years old
| 2 Children born after the family still has the same average age
| Assuming that the child is under the age of 2 years, the difference
| The current age of the children, find?
:
The present ages of the four original members of the family, a,b,c,d
The two children born later; e & f
Let f < 2 yrs, as it says
therefore
f = 1 yr old
:
Av 10 yrs ago

multiply both sides by 4, simplify
a + b + c + d - 40 = 96
a + b + c + d = 96 + 40
a + b + c + d = 136, their total age now
:
Therefore we can write the equation including the two late born children
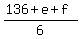 = 24 = 24
multiply both sides by 6
136 + e + f = 144
e + f = 144 - 136
e + f = 8 yrs
we know that f is 1 yr old
e + 1 = 8
e = 7 yrs old
:
the difference: 6 yrs in the last two children
| The current age of the children, ages 7 and 1
|
|
|