Question 1012290: Jen, Kathy, and Lou work Together. The ratio of Jen's salary to Kathy's salary is 4:3. Lou makes $4,000 more than Kathy does. If the total of their salaries is $134,000, how much does each person make?
Found 2 solutions by fractalier, ikleyn:
Answer by fractalier(6550)   (Show Source): (Show Source):
You can put this solution on YOUR website! Call Jen's, Kathy's, and Lou's salary, J, K, and L.
Then we have
J/K = 4/3 or J = (4/3)K
We also have
L = K + 4000
Then if J + K + L = 134,000
we can substitute in for J and L and get
(4/3)K + K + (K + 4000) = 134000
Putting the K's together, we have
(10/3)K + 4000 = 134000
(10/3)K = 130000
Now multiply by 3/10 and get
K = 39000
Thus
L = 43000
and
J = (4/3)(39000) = 52000
Checking...
39000+43000+52000=134000
Answer by ikleyn(52797)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
Jen, Kathy, and Lou work Together. The ratio of Jen's salary to Kathy's salary is 4:3. Lou makes $4,000 more than Kathy does.
If the total of their salaries is $134,000, how much does each person make?
----------------------------------------------------------------
Mathematical model is this system of equations
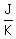 = =  , (1)
K + 4000 = L, (2)
J + K + L = 134000, (3)
or
J = , (1)
K + 4000 = L, (2)
J + K + L = 134000, (3)
or
J = 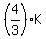 , (4)
K = L - 4000, (5)
J + K + L = 134000. (6)
Express J via L by substituting (5) into (4):
J = , (4)
K = L - 4000, (5)
J + K + L = 134000. (6)
Express J via L by substituting (5) into (4):
J = 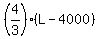 . (7)
Now substitute (7) and (5) into (6). You will get a single equation for L: . (7)
Now substitute (7) and (5) into (6). You will get a single equation for L:
 = 134000.
Multiply both sides by 3:
4*(L-4000) + 3*(L-4000) + 3L = 134000*3 = 402000.
Simplify and solve for L:
10L - 28000 = 402000 -----> 10L = 430000 -----> L = = 134000.
Multiply both sides by 3:
4*(L-4000) + 3*(L-4000) + 3L = 134000*3 = 402000.
Simplify and solve for L:
10L - 28000 = 402000 -----> 10L = 430000 -----> L =  = 43000.
Now you can easily find the rest of unknowns:
K = L - 4000 = 43000 - 4000 = 39000,
J = = 43000.
Now you can easily find the rest of unknowns:
K = L - 4000 = 43000 - 4000 = 39000,
J = 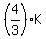 = =  = 4*13000 = 52000.
Answer. J = 52000, K = 39000, L = 43000. = 4*13000 = 52000.
Answer. J = 52000, K = 39000, L = 43000.
|
|
|