Question 797968: If one side of an equilateral triangle is along the line 12x+5y-26=0 and the opposite vertex is on the line 12x+5y+13=0, what is its area?
Answer by josgarithmetic(39623)   (Show Source): (Show Source):
You can put this solution on YOUR website! A triangle does not have any opposite vertices. Your description needs more information to restrict the third line in order to find an area.
You have two parallel lines. You can find the distance between these two lines, and this distance will be the altitude or height of an equilateral triangle.


 is one line, and is one line, and
 is the other line. is the other line.
ANY segment perpendicular to these lines, and with endpoints on these lines will serve. Let's pick point, (0,26/5) and some line of slope 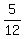 . What is the line of slope . What is the line of slope 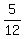 and containing point (0,26/5)? and containing point (0,26/5)?
 where y-intercept is b. where y-intercept is b.


 , but we already knew this by how we picked it. , but we already knew this by how we picked it.
The line  is perpendicular to the two given parallel lines. is perpendicular to the two given parallel lines.
WHAT POINT is the intersection of  and and  ? ?

Multiply both sides by 60,





Find the y value: 

 after all the computation and simplification. after all the computation and simplification.
We then want to use the Distance Formula to find length from (-612/25,-5) and (0,26/5). THAT WILL BE THE HEIGHT OF THE EQUILATERAL TRIANGLE.
Knowing this height, h, you can find the base of the triangle. Can you finish this?
|
|
|