Question 1203687: X: 8,9,10,11,12,13,14
Y: 1,2,3,4,5,6,7
1. ∑X ∑Y
2. ∑X²Y
3. 3∑(x+y)
Found 2 solutions by mananth, math_tutor2020:
Answer by mananth(16949)   (Show Source): (Show Source):
You can put this solution on YOUR website! X: 8,9,10,11,12,13,14
Y: 1,2,3,4,5,6,7
1. ∑X ∑Y
2. ∑X²Y
3. 3∑(x+y)
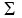 X =8 + 9 + 10 + 11 + 12 + 13 + 14 = 77 X =8 + 9 + 10 + 11 + 12 + 13 + 14 = 77
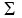 Y = 1 + 2 + 3 + 4 + 5 + 6 + 7 = 28 Y = 1 + 2 + 3 + 4 + 5 + 6 + 7 = 28
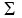 X^2=(8²) + (9²) + (10²) + (11²) + (12²) + (13²) + (14²) =875 X^2=(8²) + (9²) + (10²) + (11²) + (12²) + (13²) + (14²) =875
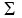 (X+Y) = 77+28 = 105 (X+Y) = 77+28 = 105
∑X ∑Y = 77*28=
∑X²Y= 875*28
3∑(x+y) = 3*105=
Answer by math_tutor2020(3828)   (Show Source): (Show Source):
You can put this solution on YOUR website!
Tutor @mananth is mostly correct.
The only mistake is ∑(X²Y)= 875*28 is false
We cannot say ∑(X²Y) = ∑X²*∑Y because ∑(A*B) = ∑A*∑B isn't true.
Consider the small sets
A = {1,2,3}
B = {4,5,6}
They have these sums
∑A = 1+2+3 = 6
∑B = 4+5+6 = 15
Then,
C = A*B = pairwise multiplication
C = {1*4, 2*5, 3*6}
C = {4,10,18}
∑C = 4+10+18 = 32
But,
∑A*∑B = 6*15 = 90
which does not match with ∑C = 32
This is one counter-example to show why ∑A*∑B = ∑(A*B) is false.
This is how I would compute ∑(X²Y)
| x | y | x^2 | x^2y | | 8 | 1 | 64 | 64 | | 9 | 2 | 81 | 162 | | 10 | 3 | 100 | 300 | | 11 | 4 | 121 | 484 | | 12 | 5 | 144 | 720 | | 13 | 6 | 169 | 1014 | | 14 | 7 | 196 | 1372 |
I recommend using a spreadsheet.
Then we sum the items in the X²Y column:
64 + 162 + 300 + 484 + 720 + 1014 + 1372 = 4116
This value is not equal to the result of 875*28.
Therefore, ∑(X²Y) = 4116
|
|
|