SOLUTION: Three resistors, of 40 Ω, 60 Ω, and 120 Ω are connected in parallel and this parallel group is connected with 15 Ω in series with 25 Ω. The whole system is then connected to a

Algebra ->  Testmodule -> SOLUTION: Three resistors, of 40 Ω, 60 Ω, and 120 Ω are connected in parallel and this parallel group is connected with 15 Ω in series with 25 Ω. The whole system is then connected to a      Log On


   

Question 1192963: Three resistors, of 40 Ω, 60 Ω, and 120 Ω are connected in parallel and this parallel group is connected with 15 Ω in series with 25 Ω. The whole system is then connected to a 120 V source. Determine (a) the I in 25 Ω, (b) the potential drop across the parallel group, (c) the potential across the 25 Ω, (d) the I in the 60 Ω, and (e) the I in 40 Ω.
Answer by ikleyn(52786) About Me  (Show Source):
You can put this solution on YOUR website!
.
Three resistors, of 40 Ω, 60 Ω, and 120 Ω are connected in parallel and this parallel group
is connected with 15 Ω in series with 25 Ω. The whole system is then connected to a 120 V source.
Determine (a) the I in 25 Ω, (b) the potential drop across the parallel group,
(c) the potential across the 25 Ω, (d) the I in the 60 Ω, and (e) the I in 40 Ω.
~~~~~~~~~~~~~~~~~ 

Resistance of the parallel group is 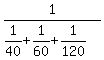 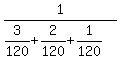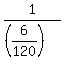1%2F%281%2F40%2B1%2F60%2B1%2F120%29 = 1%2F%283%2F120%2B2%2F120%2B1%2F120%29 = 1%2F%28%286%2F120%29%29 = 120%2F6 = 20 Ω.


So, now we can consider the circuit as a series of 20 Ω, 15 Ω and 25 Ω with the combined resistance of (20 Ω + 15 Ω + 25 Ω) = 60 Ω.


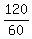Hence, the electric current  " I "  through 25 Ω (a) is 120%2F60 = 2 amperes.


        Thus question (a) is answered.


Potential drop across the parallel group is 20*2 = 40 V (b); across the 25 Ω is 25*2 = 50 V (c).


        Thus questions (b) and (d) are answered.

Solved, explained and completed.

----------------

Do not try to ask many questions in one post: it is not a way to learn subject.