SOLUTION: let f differentiable on R suppose that f^I (X) = 0 for exery x prove that f has at most one real root

Algebra ->  Testmodule -> SOLUTION: let f differentiable on R suppose that f^I (X) = 0 for exery x prove that f has at most one real root      Log On


   

Question 1164333: let f differentiable on R suppose that f^I (X) = 0 for exery x prove that f has at most one real root
Answer by ikleyn(52788) About Me  (Show Source):
You can put this solution on YOUR website!
.

I don't know what 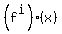 %28f%5Ei%29%28x%29 = 0 means.


It can be   an i-th degree of f(x)  or  an i-th derivative of f(x).


It is NOT CLEAR from the post and from the context, and explanations absent in the post, making its meaning DARK.


But for any of these two interpretations, the statement of the problem is INCORRECT.


A counter-example for either of the two versions is the constant function f(x) = 0  identically.


Both i-th degree and/or i-th derivative is 0 ( zero) identically, but f(x) has INFINITELY many roots, in CONTRARY to the statement.


So, the posed problem, as it is worded, printed, posted and presented, is INCORRECT.