Question 1039398: Has been struggling with these two questions in my calculus assignment, these are some derivatives releated questions.
Thankyou for the help!
A1. The equations
(1)  for r > 0
(2)  for c not equal 0
represent two different families of curves. Different values of r give different curves in (1); similarly, different values of c give different curves in (2).
Show that every curve in the family (1) is orthogonal to every curve in the family (2). That is, show that at every point of intersection, the tangents to the curves (1) and (2) are perpendicular. (Note that you are not asked to find the intersection points.) Sketch some examples of curves from both families on the same axes.
A2. A particle moves on a horizontal line so that its coordinate at time t is:
 , t larger or equal to 0
a. Find the velocity and acceleration functions.
b. When is the particle moving forward and when is it moving backward?
c. When is the particle speeding up and when is it slowing down?
Thankyou!
Answer by Fombitz(32388)   (Show Source):
You can put this solution on YOUR website! The slope of the tangent lines is equal to the value of the derivative.
So first find the derivative of each,
Implicit differentiation,
and
.
.
.
So then assume that the point intersect at ( , ).
Then,
and
.
.
The first tangent line is,
 }
The second tangent line is,
In order for the tangent lines to be perpendicular, the slopes must be negative reciprocals,
Since  ,
So they are perpendicular to each other.
.
.
.
 .
.
.
.
Differentiate,
Let's graph the derivatives to see,
 .
.
.
.
As you can see the velocity is positive for a bit and then becomes negative.
Let's find when it equals zero.
So velocity is positive or zero for 
and negative for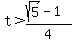 
The acceleration is always negative so the velocity steadily increases in the negative direction.
|
|
|
