Question 1035254: A2. Suppose the point (1, 2) lies on the graph of the function f.
(a) Find a point on the graph of the function  , where  .
(b) Find two points on the graph of the function 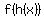 , where h(x) = x^2 −πx+ (cos^2)x.
Thankyou for looking over. Please provide some steps to steps instructions if possible.
Answer by stanbon(75887)   (Show Source):
You can put this solution on YOUR website! Suppose the point (1, 2) lies on the graph of the function f.
(a) Find a point on the graph of the function g(f(x)), where g(y)=y-1+arctan (y/2).
--------
g[f(1)] = g(2) = 2-1+arctan(2/2) = 2-1+pi/4 = 1+pi/4
Point:: (1,g(f(1)) = (1,1+pi/4)
-----------------------------------
(b) Find two points on the graph of the function f(h(x)),
where h(x) = x^2 −πx+ (cos^2)x
f[h(x)] = f[x^2-pi*x+cos^2(x)]
---
Remember f(1) = 2, so::
If x^2-pi*x+cos^2(x) = 1
then x^2-pi = 1-cos^2(x)
and x^2-pi*x = sin^2(x)
-------
So f[x^2-pi*x+cos^2(x)] = f[sin^2+cos^2] = f(1) = 2
Point:: (x,f[h(x)]) = (1,2)
-----
If x = pi
then x^2-pi*x+cos^2(x) = pi^2 - pi^2 + 1 = 1
Point:: (x,f[h(x)] (pi,2)
-------------------
Cheers,
Stan H.
--------------
Thankyou for looking over. Please provide some steps to steps instructions if possible.
|
|
|
