Question 793898: help ive got no idea where to start
There are 100 monsters. 38 of them are visible, the rest are invisible. Amongst the visible
monsters, 16 glow red, 18 glow blue, 18 glow green, 7 glow red and blue, 5 glow blue and
green and 6 glow red and green. (Note that \16 glow red" should be interpreted as: 16
monsters glow red, but each of those monsters is free to glow other colours too. The other
numbers should also be interpreted in the same way).
One day the monsters that simultaneously glow with all three colours, decide to join forces
with the invisible monsters, to form a mighty army. How many monsters are in the army?
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website! The number of visible monster is said to be  . .
The rest of the 100 monsters is  invisible monsters. invisible monsters.
There are  monsters that simultaneously glow with all three colors, and they are counted in all the other numbers given. monsters that simultaneously glow with all three colors, and they are counted in all the other numbers given.
There are also 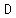 monsters that glow with exactly 2 colors. monsters that glow with exactly 2 colors.
If you add
the 16 monsters that glow red, plus
the 18 monsters that glow blue, plus
the 18 monsters that glow green
you get  . .
That count of 52 glowing monsters exceeds the number of visible monsters.
If we were counting each visible monster just once we should add up to 38.
That means that some monsters are being counted more than once in that total of  because they glow with two or three colors at once. because they glow with two or three colors at once.
The difference,  includes includes 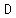 (each dual color monster counted once), plus (each dual color monster counted once), plus  (2 extra counts for each triple color monster), so (2 extra counts for each triple color monster), so

Adding the numbers of monsters that glow with at least two colors at once we get
 . That includes . That includes 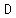 (each dual color monster counted once), plus (each dual color monster counted once), plus  because each triple color monster is counted 3 times, once for each pair of colors. because each triple color monster is counted 3 times, once for each pair of colors.
So 
 --> --> 
That might army includes the 4 triple color monsters, plus the 62 invisible ones, for a total of 

|
|
|