Question 761707: if a:b=2:3, b:c=4:5, c:d= 6:7 so find a:b:c:d?
Answer by MathLover1(20849)   (Show Source): (Show Source):
You can put this solution on YOUR website! A . . . .2 . . . . .B . . . 4 . . . . . C . . . 6
-- . = . --- . . . . -- . = . -- . . . . . -- .= .----
B . . . .3 . . . . .C . . . 5 . . . . . D . . . 7
The best way I think I can explain this is first to find the LCM of  , ,  and and  , which, of course, is , which, of course, is  . .
Now express each of the fractions above with a denominator of  . .
So,


 . . . . . . . . . ( 1 ) . . . . . . . . . ( 1 )
In the last ratio, we have  as as  . How can we express . How can we express 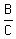 as as 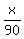 ? ?
Well,
 , so if we want to express this as , so if we want to express this as , then , then

So 
Therefore we can express 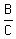 as as 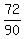 . . . . . . . . ( 2 ) . . . . . . . . ( 2 )
We have that  , and now we want to get it so that , and now we want to get it so that  is is  . .
So 
Hence 
Therefore we can express 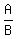 as as 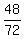 . . . . . . . . ( 3 ) . . . . . . . . ( 3 )
Collecting the three ratios ( 1 ), ( 2 ) and ( 3 ) together, we have
A . . . 48 . . . . . B . . . .72 . . . . . C . . . 90
-- . = . ---- . . . . --- . = . ---- . . . . . -- .= .-----
B . . . 72 . . . . . C . . . .90 . . . . . D . . .105
From which you can see that 
or, dividing by  , you get in lowest terms , you get in lowest terms

|
|
|