Question 1205085: 
Found 2 solutions by greenestamps, MathLover1:
Answer by greenestamps(13200)   (Show Source):
You can put this solution on YOUR website!
The given set is ((AUB)nC)U(BUD)'.
That is the union of two sets, (AUB)nC and (BUD)'. So any number in either of those two sets is in the given set.
The set (AUB)nC contains exactly the numbers that are in C AND in either A OR B. From the diagram, those numbers are 4, 5, 6, 8, 9, and 10.
The set (BUD)' contains exactly the numbers that are NOT in the union of B and D -- i.e., all the numbers that NOT in B AND NOT in D. From the diagram, those numbers are 1, 4, and 7.
Then the given set, which is the union of those two sets, contains the numbers 1, 4, 5, 6, 7, 8, and 9.
The sum of those numbers is
ANSWER: 40
------------------------------------------------------------
After getting a message from the student that my answer was wrong, I looked again and found he is right. I lost track of the number 10, which is in the set (AUB)nC.
The given set contains the numbers 1, 4, 5, 6, 7, 8, 9, and 10; the sum of those numbers is
ANSWER: 50
Answer by MathLover1(20849)  (Show Source):
You can put this solution on YOUR website!
 = , , , , , , ,
 =, ,, ,, ,,
 =,,, ,,,,
 =,,,,,,,
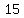
( U )=,,,,,,,,,
( U ) ∩ = , , , , , ,
( U )=, , , , , , , , , , ,
(( U ) ∩ ) U ( U )= ,,,,,,,,,,,,
the sum=
|
|
|
