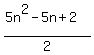You can
put this solution on YOUR website!
The first centered pentagonal number is the number of dots in an array consisting of a single dot:
P(1) = 1
To get from the first centered pentagonal number to the second, you add a pentagon around the center dot in which each side of the pentagon is made up of 2 dots. The number of dots needed to add that pentagon is 5.
P(2) = P(1)+5 = 1+5 = 6
To get from the second centered pentagonal number to the third, you add a second pentagon around the the first pentagon in which each side of the pentagon is made up of 3 dots. The number of dots needed to add that pentagon is 10.
P(3) = P(2)+10 = 6+10 = 16
The number of dots in each added pentagon is 5 more than the number in the previous pentagon. This gives us a function with a second difference of 5:
1 6 16 31 56 pentagonal numbers
5 10 15 20 first differences
5 5 5 second differences
A constant second difference tells us the formula for the n-th centered pentagonal number is a polynomial of degree 2.
There are many ways to determine that formula. I will show an unusual method....
The method of finite differences tells us that a constant second difference of 5 means the polynomial function is quadratic with a leading coefficient of 5/2.
To determine the formula for the n-th centered pentagonal number, we can compare the value of (5/2)n^2 to the value of the n-th centered pentagonal number to determine the linear function that is the rest of the formula.
n (5/2)n^2 P(n) difference
-------------------------------------
1 5/2 1 -3/2
2 10 6 -4 = -8/2
3 45/2 16 -13/2
The sequence of differences is produced by the linear function (2-5n)/2. So the formula for the n-th centered pentagonal number is

or