Question 1180157: Determine the nth term formula for the following polygonal numbers in the nth figure: (a)
heptagonal number and (b) octagonal number.
Answer by greenestamps(13200)   (Show Source):
You can put this solution on YOUR website!
A few basic facts about polygonal numbers that you can use to answer questions like this....
Let k be the number of sides of the polygon. Then
(1) In any sequence of polygonal numbers, the first two numbers in the sequence are 1 and k:
triangular numbers: 1, 3, ...
square numbers: 1, 4, ...
pentagonal numbers: 1, 5, ...
(2) The formula for the n-th term in the sequence of polygonal numbers for any value of k is a quadratic polynomial, so the sequence has a constant second difference. That constant second difference is k-2.
We can demonstrate that with the familiar triangular and square numbers:
1 3 6 10 15 the first few triangular numbers
2 3 4 5 first differences
1 1 1 the constant second difference is k-2=3-2=1
1 4 9 16 25 the first few square numbers
3 5 7 9 first differences
2 2 2 the constant second difference is k-2=4-2=2
We can use the above facts to form the sequence of heptagonal and octagonal numbers. Then, knowing that the sequence is produced by a quadratic function, we can determine that function in each case. To determine a quadratic function, we need three numbers in the sequence; so we only need to find the third number in the sequence.
Heptagonal numbers....
The first two numbers are 1 and 7; and the common second difference is 7-2=5:
1 7 ?
6 ?
5
working back up the array will give us the third pentagonal number:
1 7 18
6 11
5
We can now find the formula for the n-th heptagonal number in the form
knowing that t(1)=1, t(2)=7, and t(3)=18.
(NOTE: If you know a bit about the method of finite differences, you know that the coefficient of the quadratic term is going to be the constant second difference, divided by 2!=2 -- i.e., for this sequence the leading coefficient a will be 5/2.)
 (there is the leading coefficient we knew we were going to get)
The formula for the n-th heptagonal number is
or
Octagonal numbers....
The first two numbers are 1 and 8; and the common second difference is 8-2=6:
1 8 ?
7 ?
6
I will hope that you have enough interest in learning from this that you will go from here following the same process as shown above for the heptagonal numbers to finish the problem for octagonal numbers.
work back up the array to find the third octagonal number
use the first three octagonal numbers to form three equations to solve for the coefficients a, b, and c of the quadratic formula for the n-th octagonal number.
You should end up with this formula for the n-th octagonal number: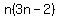 
And if you are REALLY interested in learning some cool math, write the formula for the n-th octagonal number in this form: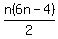 
And then observe this fascinating pattern:
n-th triangular number: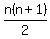 
n-th square number: 
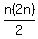n-th pentagonal number:
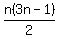n-th hexagonal number: 
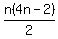n-th heptagonal number:
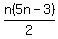n-th octagonal number:
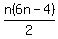n-th nonagonal number: 
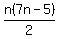n-th decagonal number: 
...
|
|
|
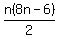