Question 1167141: Let U = {x ∈ Z | 0 ≤ x ≤ 20}. Also, let A = set of all even integers;
B= set of all prime numbers; C = set of all numbers coprime with 2; and
D={y ∈ U | y = 2z + 3, for some z∈Z}.
Represent sets A, B, C, D using set-roster notation.
Answer by Edwin McCravy(20055)   (Show Source):
You can put this solution on YOUR website!
U = {x ∈ Z | 0 ≤ x ≤ 20} = {0,1,2,3,...,20};
A = set of all even integers =  ;
B= set of all prime numbers =  ;
C = set of all numbers coprime with 2 =  ;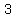
{y ∈ U | y= 2z + 3, for some z∈Z}
To do the last one:
Solve for z in the middle.
Subtract 3 from all three sides:
Divide all three sides by 2
Since z is an integer,
 = {-1,0,1,2,3,...,8}, substitute each
in 2z+3:
{y ∈ U | y = 2z + 3, for some z ∈ Z} = {1,3,5,7,...,19}
Edwin
|
|
|
