Question 1157621: Solve the following problems completely and logically.
Problem 1: Construct a difference table to determine the next term in the sequence
17,15,25,53,105,18, ___.
Problem 2: Determine the nth-term formula for the number of square tiles
in the nth figure. Then use this to find the number of square tiles
in the 30th figure.
a1=2squares, a2=4squares, a3=6squares, a4=8squares, a5=10squares
Problem 3: One straight cut across a pizza produces 2 pieces. Two cuts can produce a
maximum of 4 pieces. Three cuts can produce a maximum of 7 pieces. Four cuts can produce
a maximum of 11 pieces. Find the maximum number of pieces that can be produced
Answer by greenestamps(13216)   (Show Source): (Show Source):
You can put this solution on YOUR website!
Problem 1....
I will ignore the last number in the sequence you show, since it is almost certainly a typo.
(By the way, it would be polite of you to make sure the problem is correct before you post it....)
So I will use the first five of the terms you show and use those to find the correct 6th term and the new 7th term.
17 15 25 53 105
-2 10 28 52
12 18 24
6 6
The row of third differences is constant. To find two more terms in the sequence, add two more 6's in that row and work back up the array.
17 15 25 53 105 187 305
-2 10 28 52 82 118
12 18 24 30 36
6 6 6 6
ANSWERS: the correct 6th term is 187; the 7th term is 305.
Problem 2....
a1=2; a2=4; a3=6; a4=8; a5=10...
Clearly the nth term is 2n; a30 = 60
Problem 3....
(Note your statement of the problem is not complete....)
The numbers of regions for 1, 2, 3, and 4 cuts are
2, 4, 7, 11
Compare this sequence to the sequence of triangular numbers:
1, 3, 6, 10
The numbers in this sequence are each 1 more than the corresponding triangular number.
The formula for the n-th triangular number is 
The formula for the maximum number of pieces of pizza with n cuts is 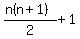
|
|
|