Question 1126619: If A = {all prime numbers between 1 and 100}, B = {2,4,6,...,98,100}, and C = {3,6,9,...,96,99}, how many elements does (A union B) intersection C have?
Found 2 solutions by MathLover1, ikleyn:
Answer by MathLover1(20849)   (Show Source): (Show Source):
You can put this solution on YOUR website!
all prime numbers between 1 and 100
A={2 ,3 , 5 ,7 , 11,13 , 17 , 19 , 23 , 29, 31 , 37 , 41, 43 ,47 ,53 ,59 , 61 ,67,71 }... (25 primes)
B = {2, 4, 6, 8, 10, 12, 14, 16, 18, 20, 22, 24, 26, 28, 30, 32, 34, 36, 38, 40, 42, 44, 46, 48, 50, 52, 54, 56, 58, 60, 62, 64, 66, 68, 70, 72, 74, 76, 78, 80, 82, 84, 86, 88, 90, 92, 94, 96, 98, 100}
( A U B ) The union of two sets is the set of elements contained in both sets.
( A U B )={2, 3,4,5, 6,7, 8, 10,11, 12,13, 14, 16,17, 18,19, 20, 22, 23,24, 26, 28,29, 30,31, 32, 34, 36, 37,38, 40, 41,42,43, 44, 46,47, 48, 50, 52, 53,54, 56, 58, 59,60,61, 62, 64, 66, 68, 70, 71,72, 74, 76, 78, 80, 82, 84, 86, 88, 90, 92, 94, 96, 98, 100}
C = {3, 6, 9, 12, 15, 18, 21, 24, 27, 30, 33, 36, 39, 42, 45, 48, 51, 54, 57, 60, 63, 66, 69, 72, 75, 78, 81, 84, 87, 90, 93, 96, 99}
( A U B ) ∩ C
look for the elements you can find in both (A U B) and C: the intersection of two sets is the set of elements that are common to both sets
I will highlight elements that are common
A U B={2,  ,4,5, ,4,5,  ,7, 8, 10,11, ,7, 8, 10,11,  ,13, 14, 16,17, ,13, 14, 16,17,  ,19, 20, 22, 23, ,19, 20, 22, 23, , 26, 28,29, , 26, 28,29,  ,31, 32, 34, ,31, 32, 34,  , 37,38, 40, 41, , 37,38, 40, 41, ,43, 44, 46,47, ,43, 44, 46,47,  , 50, 52, 53,54, 56, 58, 59, , 50, 52, 53,54, 56, 58, 59, ,61, 62, 64, ,61, 62, 64, 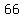 , 68, 70, 71, , 68, 70, 71, , 74, 76, , 74, 76, 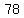 , 80, 82, , 80, 82,  , 86, 88, , 86, 88,  , 92, 94, , 92, 94, 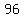 , 98, 100} , 98, 100}
C= {  , ,  , 9, , 9,  , 15, , 15,  , 21, , 21,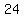 , 27, , 27,  , 33, , 33,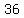 , 39, , 39,  , 45, , 45,  , 51, 54, 57, , 51, 54, 57,  , 63, , 63, 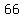 , 69, , 69,  , 75, , 75, 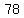 , 81, , 81,  , 87, , 87,  , 93, , 93,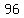 , 99} , 99}
so,
( A U B ) ∩ C={  , ,  , , , ,  , ,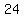 , , , , 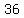 , , , , , , , ,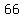 , , , , 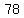 , ,  , ,  , ,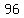 } }
( A U B ) ∩ C have  elements elements
Answer by ikleyn(52779)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
Let's do it in more simple way.
From the elementary set theory, {(A U B) n C}}} = {(A n C) U (B n C)}.
{(A n C)} is the set of all prime numbers between 1 and 100 intersected with the set of all integer numbers multiple 3 in this domain.
So, {{A n C)} consists of one single element {3}.
{(B n C)} is the set of all even numbers between 1 and 100 intersected with the set of all integer numbers multiple of 3 in this domain.
So, {(B n C)} is the set of all multiple of 6 between 1 and 100 inclusively.
Therefore,
{(A U B) n C}}} = {(A n C) U (B n C)} = the set of all multiple of 6 between 1 and 100 inclusively PLUS the number 3.
The amount of all integers multiple of 6 between 1 and 100 inclusively is 16 (because 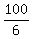 = 16.66. . . ).
Plus that single "3" gives you the answer of 17. = 16.66. . . ).
Plus that single "3" gives you the answer of 17.
-------------
The tutor @MathLover1 missed the number "54" in her final list.
|
|
|