SOLUTION: In a class of 60 students, the number of students who passed Biology is 6 more than the number of students who passed Chemistry. Every student passed at least one of the two subje

Algebra ->  sets and operations -> SOLUTION: In a class of 60 students, the number of students who passed Biology is 6 more than the number of students who passed Chemistry. Every student passed at least one of the two subje      Log On


   

Question 1106293: In a class of 60 students, the number of students who passed Biology is 6 more than the number of students who passed Chemistry. Every student passed at least one of the two subjects and 8 students passed both subjects. a. illustrate this information on a venn diagram. b. How many students passed i. chemistry ii. Biology iii. only chemistry iv. only Biology Find the percentage of the students who passed exactly one subject only
Answer by ikleyn(52781) About Me  (Show Source):
You can put this solution on YOUR website!
.
Let me show you how to solve the problem WITHOUT using a Venn diagram. 

Let B be the number of students who passed the Biology   exam only.

Let C be the number of students who passed the Chemistry exam only.


Then your first equation is  

B + C + 8 = 60      (1)    ("Every student passed at least one of the two subjects and 8 students passed both subjects.")


Your second equation is 

(B+8) - (C+8) = 6   (2)    ("the number of students who passed Biology is 6 more than the number of students who passed Chemistry")



Simplify equations (1) and (2). You will get

B + C = 52,          (1')
B - C =  6.          (2')


Now add equations (1) and (2). You will get

2B = 52 + 6 = 58  ====>  B = 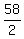58%2F2 = 29.


Then  from (1')  C = 52 - 29 = 23.


Answer.  29 students passed Biology only.

         23 students passed Chemistry only.

         29+8 = 37 passed Biology   (of them, 8 passed both).

         23+8 = 31 passed Chemistry (of them, 8 passed both).

Solved.