Tutors Answer Your Questions about sets-and-operations (FREE)
Question 1171361: Q1) Let U={a,b,c,d,e,f,g,h,i,j},A={a,b,c,d,e},B={a,b,d,f,g},C={a,d,e} Findl
(A⨁C)\B
(A\C)∩(B\C)
n(A^c∪B^c )
Answer by CPhill(1959)   (Show Source):
You can put this solution on YOUR website! Let $U = \{a, b, c, d, e, f, g, h, i, j\}$, $A = \{a, b, c, d, e\}$, $B = \{a, b, d, f, g\}$, and $C = \{a, d, e\}$.
1. **(A ⊕ C) \ B**
* $A \oplus C = (A \setminus C) \cup (C \setminus A)$
* $A \setminus C = \{b, c\}$
* $C \setminus A = \emptyset$
* $A \oplus C = \{b, c\} \cup \emptyset = \{b, c\}$
* $(A \oplus C) \setminus B = \{b, c\} \setminus \{a, b, d, f, g\} = \{c\}$
2. **(A \ C) ∩ (B \ C)**
* $A \setminus C = \{b, c\}$
* $B \setminus C = \{b, f, g\}$
* $(A \setminus C) \cap (B \setminus C) = \{b, c\} \cap \{b, f, g\} = \{b\}$
3. **n(Ac ∪ Bc)**
* $A^c = U \setminus A = \{f, g, h, i, j\}$
* $B^c = U \setminus B = \{c, e, h, i, j\}$
* $A^c \cup B^c = \{c, e, f, g, h, i, j\}$
* $n(A^c \cup B^c) = |A^c \cup B^c| = 7$
Therefore:
* (A ⊕ C) \ B = {c}
* (A \ C) ∩ (B \ C) = {b}
* n(Ac ∪ Bc) = 7
Question 1177473: II. A survey was done of 200 8-year olds asking if they like certain types of vegetables (broccoli, carrots, and green beans). The following were obtained.
28 kids only liked green beans.
73 kids liked broccoli.
40 kinds liked broccoli and green beans.
79 kids liked exactly 2 of these vegetables.
12 kinds liked broccoli and carrots, but not green beans.
34 kinds only liked carrots.
104 kids liked carrots or green beans, but not broccoli.
1. How many kids liked carrots, but not green beans?
2. How many kids liked exactly 1 of the three vegetables?
3. How many kids do not like carrots?
Found 2 solutions by MathTherapy, CPhill:
Answer by MathTherapy(10552)  (Show Source):
You can put this solution on YOUR website!
II. A survey was done of 200 8-year olds asking if they like certain types of vegetables (broccoli, carrots, and green beans). The following were obtained.
28 kids only liked green beans.
73 kids liked broccoli.
40 kinds liked broccoli and green beans.
79 kids liked exactly 2 of these vegetables.
12 kinds liked broccoli and carrots, but not green beans.
34 kinds only liked carrots.
104 kids liked carrots or green beans, but not broccoli.
1. How many kids liked carrots, but not green beans?
2. How many kids liked exactly 1 of the three vegetables?
3. How many kids do not like carrots?
"RESPONDENT'S" answers are WRONG!!
Correct answers:
1. How many kids liked carrots, but not green beans? 34 + 12 = 46
2. How many kids liked exactly 1 of the three vegetables? 21 + 34 + 28 = 21 + 62 = 83
3. How many kids do not like carrots? 21 + 25 + 28 = 21 + 53 = 74
Answer by CPhill(1959) (Show Source):
You can put this solution on YOUR website! It's helpful to solve this kind of problem with a Venn Diagram. Here's how we can approach this:
**1. Draw a Venn Diagram**
Draw three overlapping circles representing broccoli, carrots, and green beans.
**2. Fill in the Diagram**
* **28 kids only liked green beans:** Place "28" in the green beans only section.
* **40 kids liked broccoli and green beans:** Since 73 like broccoli total, and 40 like broccoli and green beans, 73 - 40 = 33 like only broccoli and green beans. Of those, 12 also like carrots. So, place "12" in the broccoli-carrot-green bean overlap, and 33 - 12 = 21 in the broccoli-green bean overlap.
* **79 kids liked exactly 2 of these vegetables:** We've already accounted for 12 who like broccoli and carrots, and 21 who like broccoli and green beans. So, 79 - 12 - 21 = 46 must like carrots and green beans only.
* **12 kids liked broccoli and carrots, but not green beans:** Place "12" in the broccoli-carrot overlap.
* **34 kids only liked carrots:** Place "34" in the carrots only section.
* **104 kids liked carrots or green beans, but not broccoli:** This includes those who like only carrots, only green beans, and the overlap between carrots and green beans. We've already accounted for 28 + 46 = 74, so 104 - 74 = 30 must like carrots only.
**3. Calculate the Remaining Values**
* **Total who like carrots:** 30 (carrots only) + 12 (broccoli-carrot) + 46 (carrot-green bean) + 12 (all three) = 100
* **Total who like any vegetable:** Add up all the numbers in the Venn diagram.
* **Those who dislike carrots:** 200 (total) - 100 (like carrots) = 100
**Answers**
1. **How many kids liked carrots, but not green beans?** 30 (carrots only) + 12 (broccoli-carrot) = 42
2. **How many kids liked exactly 1 of the three vegetables?** 30 (carrots only) + 28 (green beans only) + 12 (broccoli and carrots only) = 70
3. **How many kids do not like carrots?** 100
Question 1177472: . 50 people were surveyed about whether they like the ice cream flavors vanilla and strawberry. 20 people liked vanilla, 25 people liked strawberry, and 30 people liked vanilla or strawberry.
1. How many people like vanilla and strawberry?
2. How many people like exactly one of these two flavors?
3. How many people liked strawberry or did not like vanilla?
Answer by CPhill(1959) (Show Source):
You can put this solution on YOUR website! **1. People who like vanilla and strawberry**
We can use the principle of inclusion-exclusion to find the number of people who like both vanilla and strawberry:
* Total who like vanilla or strawberry = Total who like vanilla + Total who like strawberry - Total who like both
Plugging in the given values:
* 30 = 20 + 25 - Total who like both
Solving for the number who like both:
* Total who like both = 20 + 25 - 30 = 15
**Therefore, 15 people like both vanilla and strawberry.**
**2. People who like exactly one flavor**
* People who like only vanilla: 20 (total who like vanilla) - 15 (who like both) = 5
* People who like only strawberry: 25 (total who like strawberry) - 15 (who like both) = 10
So, 5 + 10 = **15 people like exactly one of the two flavors.**
**3. People who liked strawberry or did not like vanilla**
* People who did not like vanilla: 50 (total people) - 20 (who like vanilla) = 30
* People who liked strawberry only: 10 (from previous calculation)
Since we want those who liked strawberry *or* did not like vanilla, we need to be careful not to count those who like both twice. So, we use the principle of inclusion-exclusion again:
* Total who liked strawberry or did not like vanilla = Total who liked strawberry + Total who did not like vanilla - Total who liked strawberry and did not like vanilla
The last group is the same as those who liked strawberry only. Therefore:
* Total who liked strawberry or did not like vanilla = 25 + 30 - 10 = 45
**Therefore, 45 people liked strawberry or did not like vanilla.**
Question 1180160: Anna is a teacher and her cousins are a banker, a salesperson, and an engineer. All of them
sit around a table. Anna sits on Melody's left. Chinky sits at the banker's right. Katherine, who
faces Melody, is not the salesperson. Determine the seating arrangement of the cousins.
Answer by ikleyn(52778)  (Show Source):
You can put this solution on YOUR website! .
Anna is a teacher and her cousins are a banker, a salesperson, and an engineer.
All of them sit around a table.
(a) Anna sits on Melody's left.
(b) Chinky sits at the banker's right.
(c) Katherine, who faces Melody, is not the salesperson.
Determine the seating arrangement of the cousins.
~~~~~~~~~~~~~~~~~~~~~~~~~
(1) In the Figure below, I placed 4 symbols "around a circle table".
"A" is Ann. There is only one place at the table, where "Anna sits on it left".
Hence, this place is for Melody, and I marked it M. And we know that Chinky is not a salesperson.
A (teacher)
M Y
X
Figure 1.
Two other persons are unknown now. I marked them X and Y in the figure.
Obviously, X and Y are either Chinky or Katherine - we don't know who of them is X and who is Y.
(2) Condition (c) says "Katherine, who faces Melody, is not the salesperson".
It means X = Katherine (K), and I update this information in the next figure.
A (teacher)
M Y
K (not a salesperson)
Figure 2.
(3) Hence, Y is Chinky (the only possibility left),
and I update this information in the next figure.
A (teacher)
M C
K (not a salesperson)
Figure 3.
+----------------------------------------------+
| Thus the seating arrangement of cousins |
| is determined completely in Figure 3. |
+----------------------------------------------+
**********************************************************************
We can make one step forward and to learn more about their occupations.
Condition (b) says "Chinky sits at the banker's right".
Hence, from the Figure 3, K, or Katherine, is the baker.
A (teacher)
M C
K (banker)
Figure 4.
We have no more information to complete with their occupation.
Solved.
Question 1209653: Set a question to prove that (AUB)UC=AU(BUC)
Answer by CPhill(1959) (Show Source):
Question 1208798: Let A and B be two sets containing 4 and 2 elements respectively. Then the number of subsets of the set AxB, each having at least three elements is
A. 219
B. 228
C. 235
D. 256
Answer by math_tutor2020(3816) (Show Source):
You can put this solution on YOUR website!
Construct two example sets
A = {a, b, c, d}
B = {e, f}
A x B = cartesian product
A x B = set of ordered pairs of form (p,q) where p is from set A and q is from set B
A x B = {
(a,e), (a,f),
(b,e), (b,f),
(c,e), (c,f),
(d,e), (d,f)
}
If you want you can flatten the set into one single line like this
A x B = { (a,e), (a,f), (b,e), (b,f), (c,e), (c,f), (d,e), (d,f) }
But it might be preferable to have it broken up into rows.
4 items in set A, 2 items in set B, n = 4*2 = 8 ordered pairs in AxB.
There are 2^n = 2^8 = 256 possible subsets of AxB (see Power Set)
This includes the set AxB itself and the empty set.
Refer to Pascal's Triangle. Look at the row that starts with "1,8,28...". Each value in Pascal's Triangle can be computed using the nCr combination formula.
All of those values in that row add to 256.
The first three items of this row correspond to:- 1 empty set
- 8 subsets that are singletons. These are the subsets that have exactly one ordered pair.
- 28 subsets that have two ordered pairs
Add up those first three values to get 1+8+28 = 37
There are 37 subsets with at most 2 ordered pairs.
Then 256-37 = 219 is the amount of subsets that have between 3 ordered pairs and 8 ordered pairs.
Answer: Choice A
Question 1208676: Why is the cardinality of the empty set { Ø } equal zero?
Found 3 solutions by math_tutor2020, greenestamps, ikleyn:
Answer by math_tutor2020(3816) (Show Source):
Answer by greenestamps(13200)  (Show Source):
You can put this solution on YOUR website!
The cardinality of a set is the number of elements in the set.
The number of elements in the empty set is 0, so the cardinality of the empty set is zero.
Answer by ikleyn(52778) (Show Source):
You can put this solution on YOUR website! .
The cardinality of the empty set is zero, because the empty set has zero elements.
All these profound exercises about empty set remind me
the expression "treading water in a mortar".
Question 1208679: What is the cardinality of set F?
F = { { Ø }, (x + y), 1/4, 1/3, 1/2, A, B, C, D }
What do I see inside the bigger set?
I see 9 elements.
The cardinality is 9.
Do you agree?
Answer by Edwin McCravy(20054)  (Show Source):
You can put this solution on YOUR website!
F = { { Ø }, (x + y), 1/4, 1/3, 1/2, A, B, C, D }
Yes, the 9 elements of F are
1. { Ø }
2. (x + y)
3. 1/4
4. 1/3
5. 1/2
6. A
7. B
8. C
9. D
So you are right, the cardinality (count) is 9.
Comment:
The set { Ø } is not empty because it contains one element, the empty set Ø.
And Ø is only an element of { Ø } and not an element of F.
The element (x + y) is a single number depending upon what number x and y are.
Edwin
Question 1208677: What is the cardinality of set R?
R = { {1, 2, 3,} {A, B, C} }
I see two sets inside a bigger set. What I see is the key word.
I say the cardinality is 2.
You say?
Answer by ikleyn(52778) (Show Source):
You can put this solution on YOUR website! .
What is the cardinality of set R?
R = { {1, 2, 3,} {A, B, C} }
I see two sets inside a bigger set. What I see is the key word.
I say the cardinality is 2.
You say?
~~~~~~~~~~~~~~~~~~
The comma after "3" is placed in wrong place.
/////////////////////
Comment from student : Ok. I placed the command in the wrong location in the set.
Here is setbR again: R = { {1, 2, 3} , {A, B, C} } Cardinality is 2. Yes???
My response : Yes.
Question 1208678: What is the cardinality of set B?
B = {pi, e, {x, y, y} }
I see three items in set B.
I see pi, e, and another set containing elements x, y, and z
My answer is 3.
The cardinality is 3.
You say?
Answer by ikleyn(52778) (Show Source):
You can put this solution on YOUR website! .
In your post, you write
"I see pi, e, and another set containing elements x, y, and z ".
I do not see it.
What I see is pi, e, and the list {x,y,y} in curved brackets,
which contradicts to the rules of presenting sets, since the element "y" is repeated twice.
////////////////////////
Comment from student: Inside set B is another set. Let's call the other set a smaller box.
It's like opening a box and finding a ball, glove and another box. We don't know what lies inside the smaller box.
So, when I open the bigger box, I see three items: ball, glove and smaller box.
So, the cardinality is 3.
NOTE: I MADE A TYPO. THE SET INSIDE SET B SHOULD HAVE ELEMENTS X, Y, AND Z NOT X, Y, AND Y.
WE DON'T REPEAT THE ELEMENTS IN A SET. YOU SAY?
My response: Correct.
Question 1208675: What is the cardinality of set A?
A = {4, 5, 6, 7, 8}
I say 5.
You say?
Answer by ikleyn(52778) (Show Source):
Question 1208384: Let N be the set of the four gospels. Use the Roster Method to represent the four gospels of the New Testament.
Let N be a set.
N = {Matthew, Mark, Luke, John}
Is this the correct way to apply the roster method in set theory?
Found 2 solutions by ikleyn, math_tutor2020:
Answer by ikleyn(52778) (Show Source):
You can put this solution on YOUR website! .
If you want to be precisely correct, then instead "Let N be a set", as written in your post,
you should write "Let N be the set of the four gospels", as it is written in the problem.
Answer by math_tutor2020(3816) (Show Source):
You can put this solution on YOUR website!
Yes you are correct. Roster notation is listing out each item of the set. Each member is listed exactly once.
The order of the members doesn't matter.
Question 1208383: Why can't the elements of a set repeat?
Sample
A = {4, 5, 6, 5} is wrong because number 5 repeats.
Why is it not ok for 5 to repeat?
Found 2 solutions by ikleyn, Edwin McCravy:
Answer by ikleyn(52778) (Show Source):
You can put this solution on YOUR website! .
Why can't the elements of a set repeat?
~~~~~~~~~~~~~~~~~~~~
This is a rule for representing/enumerating elements of a set,
established in Mathematics by mathematicians as a general agreement.
Not a subject to discussion by other mortals -
- only the subject to follow this rule strictly.
It's like an accountant in his transaction ledger will not record the same transaction twice.
If he will do it, he will lose his job.
Answer by Edwin McCravy(20054) (Show Source):
You can put this solution on YOUR website!
In mathematics, there is only one number that is labeled "5" or "five" or "V".
A = {4, 5, 6, 5} is not "wrong", it's simply not the simplest way to
write A = {4, 5, 6}.
Writing 2+3 is not "wrong", it's just simpler written as 5.
Edwin
Question 1208382: As I understand it, the cardinality of a set is the number of elements in a set.
Is this right?
Sample
A = {w, x, y, z}
The symbol for cardinality is | A |.
So, for this sample, | A | = 4.
You say?
Answer by ikleyn(52778) (Show Source):
You can put this solution on YOUR website! .
Correct.
You correctly counted the number of elements in the set
and correctly attributed it to the conception of the cardinality of the given set.
Question 1208385: Use Set-builder Notation to represent digits 0 to 9.
Let D be a set.
D = {x | x is a digit}
Is this correct in terms of set theory?
Answer by math_tutor2020(3816) (Show Source):
You can put this solution on YOUR website!
I would phrase it like this
D = {x | x is an integer and 0 ≤ x ≤ 9}
Your math textbook may write it like this
The portion  translates to "x is in the set of integers" i.e. "x is an integer".
Why is Z used for the set of integers? The Z stands for Zahl, which is a German word meaning "number".
More info found here
https://mathworld.wolfram.com/Z.html
Question 1208386: Let A and B be sets. If elements of set A are also found in set B, then A is a subset of B.
The textbook writes it this way: A ⊆ B
Sample:
A = {x, x + 1, x + 2}
B = {a, b, c, x, x + 1, x + 2}
I see that the elements in set A are also in set B.
Conclusion: A ⊆ B
You say?
Answer by math_tutor2020(3816) (Show Source):
You can put this solution on YOUR website!
You are correct. Anything inside set A is also in set B.
It might help to highlight the items you want to focus on.
A = {x, x + 1, x + 2}
B = {a, b, c, x, x + 1, x + 2}
This is what the Euler Diagram would look like
circle A is entirely inside circle B.
x,x+1,x+2 are in circle A. By extension they are also in circle B.
a,b,c are in circle B, but outside circle A.
Question 1208299: 1 Write the following in set notation:
(a) The set of all real numbers greater than 27.
(b) The set of all real numbers greater than 8 but less than 73.
2 Given the sets S_{1} = \langle2, 4, 6\rangle following statements are true? S_{2} = \langle7, 2, 6\rangle S_{3} = \langle4, 2, 6\rangle and S_{4} = \langle2, 4\rangle which of the
(a) S_{1} = S_{2}
(d) 3 \notin S_{2} deg
(g) S_{1} supset S 4
(b) S_{1} = R
(e) 4 \notin S_{4}
(h) emptyset subset S ?
(c) 5 \in S_{2}
(f) S_{4} subset R
(1) S 3 supset \langle1, 2\rangle
3 Referring to the four sets given in the preceding problem, find:
(a) S_{1} cup S 2
(c) S_{2} cap S 3
(e) S_{4} cap S 2 cap S 1
(b) S_{1} cup S 3
(d) S_{2} cap S 4
(f) S_{1} cup S 1 cup S 4
Answer by Edwin McCravy(20054) (Show Source):
You can put this solution on YOUR website!
No fair dumping a whole bunch of problems on us like that!
Here's the first one. Maybe someone else will do some others.
1 Write the following in set notation:
(a) The set of all real numbers greater than 27.
{x|x ε R, x > 27}
(b) The set of all real numbers greater than 8 but less than 73.
[Note: "it is greater than 8" is the same as saying "8 is less than it"]:
{x|x ε R, 8 < x < 73}
Edwin
Question 1208149: If two sets A and B have the same elements, then we say that A = B.
Sample 1
Set A = { 20, 30, 40 }
Set B = { 30, 40, 20 }
I conclude that A = B.
Sample 2
Set A = { red, white, blue }
Set B = { white, blue, red }
I conclude that A = B.
You say?
Answer by ikleyn(52778) (Show Source):
You can put this solution on YOUR website! .
D U P L I C A T E
It was just answered at this forum under this link
https://www.algebra.com/algebra/homework/sets-and-operations/sets-and-operations.faq.question.1208141.html
Please do not bombard us with duplicates.
Question 1208147: The set of digits consists of the following set of numbers: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9.
The textbook tells me that we can denote the set of digits using a Roster Method.
Let D = set of digits
D = { 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 }
The book goes on to say that there is a second way to denote a set. That is to use set-builder notation, where the set D of digits is written as D = { x | x is a digit }.
Questions
1. Use the Roster Method to denote the set of even digits.
Let E = set of even digits.
Textbook answer: E = { 0, 2, 4, 6, 8 }.
Why is 0 an element of set E? I thought the whole number 0 is a number without value.
2. Use Set-builder Notation to denote the set of odd digits.
Let O = set of odd digits.
0 = { x | x is an odd digits} = { 1, 3, 5, 7, 9 }
You say?
Answer by ikleyn(52778) (Show Source):
You can put this solution on YOUR website! .
(2) is close to be correct, but is not fully correct.
In order for (2) be fully correct, it should be written in the form
O = { x | x is an odd digits} = { 1, 3, 5, 7, 9 },
where symbol O in the left side is letter O (not digit "0", meaning zero).
(1) Textbook answer E = { 0, 2, 4, 6, 8 } is correct.
0 is an even digit.
///////////////////////
Question from student: Why is 0 an element of set E? I thought the whole number 0 is a number without value.
My response. It is a great mistake and a fatal error to think that zero is the absence of value.
In opposite, zero has a very specific value and expresses the absent of amount.
****************************************************************
A typical example is when in your pocket
you have neither banknotes nor coins.
Then you say that the amount of cash in your pocket is zero.
****************************************************************
When you divide zero by two in integer numbers, you obtain zero as the quotient and zero as the remainder.
It means that zero is an even number, in the row of other even integer numbers
that are divisible by two with no remainder.
Usually/normally, students learn this truth/conception in the second or third grade.
As I see from your posts, you try to review College Algebra without having necessary
elementary standard basic knowledge (prerequisites) related to the second and/or third grade.
I just made similar notices three times before, responding to your preceding posts.
So, if you want to know my opinion, it is that you should not reviewing College Algebra,
but start from Arithmetic and then continue with Pre-Algebra.
It will better correspond to your current level in Math.
Question 1208139: Use set-builder notation to denote the set of all even digits.
Let me see.
Let E = set of even digits
E = { x | x is an even digit } = { 0,2,4,6,8 }
Why is 0 an element of set E?
Found 2 solutions by math_tutor2020, ikleyn:
Answer by math_tutor2020(3816) (Show Source):
Answer by ikleyn(52778) (Show Source):
You can put this solution on YOUR website! .
Use set-builder notation to denote the set of all even digits.
Let me see.
Let E = set of even digits
(a) E = { x | x is an even digit } = { 0,2,4,6,8 }
(b) Why is 0 an element of set E?
~~~~~~~~~~~~~~~~~~~~
(a) is correct;
(b) is by definition (since 0 is an even number).
///////////////////////
Comment from student: How is zero (the absence of value) be an even number?
My response. It is a great mistake and a fatal error to think that zero is the absence of value.
In opposite, zero has a very specific value and expresses the absent of amount.
**********************************************************
A typical example is when in your pocket
you do not have neither banknotes nor coins.
**********************************************************
When you divide zero by two in integer numbers, you obtain zero as the quotient and zero as the remainder.
It means that zero is an even number, in the row of other even integer numbers
that are divisible by two with no remainder.
Usually/normally, students learn these truths/conceptions in the second or third grade.
As I see from your posts, you try to review College Algebra without having necessary
elementary standard basic knowledge (prerequisites) related to the second and/or third grade.
I just made similar notices two times before, responding to your preceding posts.
So, if you want to know my opinion, it is that you should not reviewing College Algebra,
but start from Arithmetic and then continue with Pre-Algebra.
It will better correspond to your current level in Math.
Question 1208143: Use set-builder notation to denote the set of the first 4 books in the New Testament.
Question 1
Let N = set of the first 4 books in the New Testament
I say the following:
N = { x | x is one of the first 4 books in the New Testament }
N = { Matthew, Mark, Luke, John }
You say?
Question 2
Use set-builder notation to denote the set of the first 4 books in the New Testament.
Let N = set of all 5 NYC boroughs
I say the following:
N = { x | x represents all 5 boroughs of NYC }
N = { Brookkyn, Bronx, Manhattan, Staten Island, Queens }
You say?
Found 2 solutions by math_tutor2020, ikleyn:
Answer by math_tutor2020(3816) (Show Source):
You can put this solution on YOUR website!
When you list all members of a set, you are using roster notation.
Think of a sports roster that lists all players on a team.
{ Matthew, Mark, Luke, John } is roster notation while { x | x is one of the first 4 books in the New Testament } is set-builder notation.
Set-builder notation describes the basic rule(s) to generate the roster notation.
The rules can be verbal in nature or use some kind of algebra.
An example of set-builder notation would be
{ x | x is a nonnegative even number }
which gives this roster notation
{0, 2, 4, 6, 8, 10, ...}
The triple dots mean "keep this pattern going forever".
You don't need to mention the roster notation since your teacher and/or textbook appears to not be asking for it. However, it would be good practice to do so anyway on a separate scratch piece of paper.
Your set-builder notation answer for question 1 is correct.
Question 2 somehow seems to be mixed up or blended with question 1. But if you're talking about the boroughs of NYC for question 2, then { x | x represents all 5 boroughs of NYC } is the correct set-builder notation for it.
Answer by ikleyn(52778) (Show Source):
You can put this solution on YOUR website! .
(Q1) Your answer is correct.
(Q2) Your first line in Q2 does not correspond to the rest in Q2.
/////////////////////
Comment from student: Question 2 Use set-builder notation to denote the set of 5 NYC boroughs.
Let N = set of all 5 NYC boroughs I say the following: N = { x | x represents all 5 boroughs of NYC }
N = { Brookkyn, Bronx, Manhattan, Staten Island, Queens } You say?
My response: Brookkyn (as written in your post) is INCORRECT.
The correct writing is  , with no any other versions/options/modifications/distortions/falsifications.
Question 1208140: Use the Roster Method to denote the set of all odd digits.
Let O = set of odd digits
O = { 1, 3. 5, 7, 9 }
Questions:
1. Why is 1 an element of set O?
2. Why is 9 an element of set O considering that 9 is not just divisible by 1 and itself?
Answer by ikleyn(52778) (Show Source):
You can put this solution on YOUR website! .
(1) 1 is element of O, since 1 is an odd digit.
(2) 9 is element of O, since 9 is an odd digit.
The part "considering that 9 is not just divisible by 1 and itself?"
is set of words irrelevant to question 2.
//////////////////
Comment from student: In what way is 1 an odd number? In what way is 9 an odd number?
My response: 1 is an odd number, because, when divided by 2 in integer numbers, it gives
the remainder of 1 (one). So, according to the definition of odd numbers, 1 is an odd number.
9 is an odd number, because, when divided by 2 in integer numbers, it gives
the remainder of 1 (one). So, according to the definition of odd numbers, 9 is an odd number.
Usually/normally, students learn these truths/conceptions in the second or third grade.
As I see from your posts, you try to review College Algebra without having necessary
elementary standard basic knowledge (prerequisites) related to the second and/or third grade.
If I remember correctly, I just made similar notice once before, responding to one of your preceding posts.
So, if you want to know my opinion, it is that you should not reviewing College Algebra,
but start from Arithmetic and then continue with Pre-Algebra.
It will better correspond to your current level in Math.
Question 1208141: If two sets A and B have the same elements, then we say that A = B.
Sample 1
Set A = { 20, 30, 40 }
Set B = { 30, 40, 20 }
I conclude that A = B.
Sample 2
Set A = { red, white, blue }
Set B = { white, blue, red }
I conclude that A = B.
You say?
Answer by ikleyn(52778) (Show Source):
Question 1206297: Draw a Venn diagram
(A ∩ B) ∪ (A ∩ C)
Found 2 solutions by math_tutor2020, mananth:
Answer by math_tutor2020(3816) (Show Source):
You can put this solution on YOUR website!
(A ∩ B) ∪ (A ∩ C)
The "U" symbol means "union"
Union means "or"
(A ∩ B) ∪ (A ∩ C) = (A ∩ B) or (A ∩ C)
The element is in set (A ∩ B) or set (A ∩ C) or both sets simultaneously.
Set A is present for both parts.
Therefore, this element is in set A.
We can use the distributive law to rewrite things a bit
(A ∩ B) ∪ (A ∩ C) = A ∩ (B U C)
Think of it like saying A*B + A*C = A*(B+C) where * represents set intersection and + represents set union.
Once we arrive at A ∩ (B U C), it should be more clear that the element must reside in set A.
It also resides in (B U C)
Meaning it's in B, or C, or both.
We'll shade the region in circle A that's either in B or C or both B & C.
Refer to the diagram that tutor @mananth had created to see what I mean.
Answer by mananth(16946)  (Show Source):
Question 1206300: Perform the given set operation. Let U = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10}. (Enter your answers as a comma-separated list. Enter EMPTY for the empty set.)
{4, 5, 8} ∩ {5, 8, 10}
Found 2 solutions by ikleyn, Theo:
Answer by ikleyn(52778) (Show Source):
Answer by Theo(13342)  (Show Source):
Question 1206195: A group of 2175 students were surveyed about the
courses they were taking at their college with
the following results:
1025 students said they were taking Dance.
1087 students said they were taking History.
1115 students said they were taking Math.
585 students said they were taking History and Math.
501 students said they were taking Math and Dance.
537 students said they were taking History and Dance.
243 students said they were taking all three courses.
Found 5 solutions by MathTherapy, greenestamps, Edwin McCravy, ikleyn, mccravyedwin:
Answer by MathTherapy(10552) (Show Source):
You can put this solution on YOUR website!
A group of 2175 students were surveyed about the
courses they were taking at their college with
the following results:
1025 students said they were taking Dance.
1087 students said they were taking History.
1115 students said they were taking Math.
585 students said they were taking History and Math.
501 students said they were taking Math and Dance.
537 students said they were taking History and Dance.
243 students said they were taking all three courses.
It's extremely IRRITATING as well as ANNOYING when one seeks an answer to a mathematics problem and not state
a question or directive in order to get that answer. I usually ignore these posts. However, I don't mind making
an exception and respond to this one.
Here's the Venn
 .
If you can read Venn diagrams then you shouldn't have a problem with this one. Nonetheless, I'll
clarify a few things.
M denotes Math
D denotes Dance
H denotes History
Those taking M, only: 272
Those taking M&D, only: 258
Those taking M&H, only: 342
Those taking M,D&H: 243
Those taking D, only: 230
Those taking D&H, only: 294
Those taking H, only: 208
TOTAL (those taking @ least 1 of the 3): 1,847
Those taking NONE of the 3: 2,175 - 1,847 = 328
With all this info. I agree with SIR EDWIN 100%, in that any question can be answered. Then again, and as SIR
EDWIN also pointed out, the Venn diagram may've been all that's needed. If so, that should've been stated.
SELAH!
Answer by greenestamps(13200) (Show Source):
You can put this solution on YOUR website!
To tutor @ikleyn....
How absurd -- to claim that if you weren't answering questions on this forum things would be chaos within four days. Such unmitigated arrogance.
And you ABSOLUTELY DESERVE to be put down if you post a response "ARE YOU SANE" because the student neglected to ask a question. Most tutors at this forum who are of better character than you would simply point out to the student that their post contained no question.
Answer by Edwin McCravy(20054) (Show Source):
You can put this solution on YOUR website!
Stop putting students down, Ikleyn!! They're struggling! Of course this
student is sane, silly. The main thing was to get the Venn diagram. That
may have been all he/she wanted. It is certainly enough. There may have
been several questions but any of them would be trivial once the Venn
diagram was set up.
Answer by ikleyn(52778) (Show Source):
You can put this solution on YOUR website! .
A group of 2175 students were surveyed about the
courses they were taking at their college with
the following results:
1025 students said they were taking Dance.
1087 students said they were taking History.
1115 students said they were taking Math.
585 students said they were taking History and Math.
501 students said they were taking Math and Dance.
537 students said they were taking History and Dance.
243 students said they were taking all three courses.
~~~~~~~~~~~~~~~~~~~~~~
I read attentively your post, but did not find any question in it.
Are you sane ?
/////////////////////
Edwin, there are minimal basic elementary rules of communicating at this forum.
First rule is that a post should be written clearly and correctly,
and the problem should be sensible (in opposite to be non-sensible).
Second rule is that a post must be complete and contain all necessary data.
Third rule is that a post must contain a question.
Fourth rule is that a post should contain reasonable finite number of questions
(the best one question, the most - three inter-related questions, but not 6 or 8 questions).
These rules are simple and necessary, and I ALWAYS will insist that they be followed.
You, from your side, apply 1000-ton efforts to break them and to put me down.
Please stop breaking these rules. Also, please stop putting me down.
Next, why do you think that they want to learn from you about Venn diagram ?
May be, in opposite, they want to learn from ME about Inclusion-Exclusion principle ?
I am the ONLY ONE person at this forum, who supports some order here, during the years.
Without me, it will be MESS in two weeks.
Did I say " in two weeks " ? - No, not in two weeks. - In four days.
Answer by mccravyedwin(407)  (Show Source):
You can put this solution on YOUR website! A group of 2175 students were surveyed about the courses
they were taking at their college with the following results:
Put the 8 clues in reverse order, for that's the order you need them.
1. 243 students said they were taking all three courses.
2. 537 students said they were taking History and Dance.
3. 501 students said they were taking Math and Dance.
4. 585 students said they were taking History and Math.
5. 1115 students said they were taking Math.
6. 1087 students said they were taking History.
7. 1025 students said they were taking Dance.
8. 2175 students were surveyed
Draw a Venn diagram with three overlapping circles, labeled D, H, and M,
all inside a big rectangle.
1. 243 goes in the very center region which is common to all 3 circles.
2. 537-243=294 were taking History and Dance but not Math.
3. 501-243=258 were taking Math and Dance but not History.
4. 585-243=342 were taking History and Math but not Dance.
5. 1115-258-243-342=272 were taking Math only.
6. 1087-294-243-342=208 were taking History only.
7. 1025-294-243-258=230 were taking Dance only.
8. 2175-230-294-208-258-243-342-272=328 were not taking any of the three.
[These 328 go outside all three circles but inside the rectangle.
Put these 8 results in the 8 regions of a Venn diagram with three overlapping
circles but inside the big rectangle. Then you'll be ready to answer any
question they can give you.
Edwin
Question 1206204: A group of 2468 students were surveyed about the courses they were taking at their college with the following results:
1140 students said they were taking Psychology.
1244 students said they were taking Dance.
1110 students said they were taking History.
599 students said they were taking Psychology and Dance.
550 students said they were taking Psychology and History.
602 students said they were taking History and Dance.
349 students said they were taking all three courses.
a) How many students took Psychology, History, or Dance?
b) How many students took none of the courses?
c) How many students took Psychology or didn't take History?
d) How many students took Psychology or Dance, but not History?
e) How many students took Psychology & History or took History & Dance?
f) How many students took History and Dance, but not Psychology?
Answer by ikleyn(52778) (Show Source):
You can put this solution on YOUR website! .
A group of 2468 students were surveyed about the courses they were taking at their college with the following results:
1140 students said they were taking Psychology.
1244 students said they were taking Dance.
1110 students said they were taking History.
599 students said they were taking Psychology and Dance.
550 students said they were taking Psychology and History.
602 students said they were taking History and Dance.
349 students said they were taking all three courses.
a) How many students took Psychology, History, or Dance?
b) How many students took none of the courses?
c) How many students took Psychology or didn't take History?
d) How many students took Psychology or Dance, but not History?
e) How many students took Psychology & History or took History & Dance?
f) How many students took History and Dance, but not Psychology?
~~~~~~~~~~~~~~~~~~~~~~
(a) For (a), use the Inclusion-Exclusion principle.
It says that the number of elements in the union of three subset P, D and H is the sum
of numbers of elements in the separate sets MINUS the number of element in each of their
in-pair intersections PLUS the number of elements in the triple intersection.
According to this formula, n(P U H U D) = 1140 + 1244 + 1110 - 599 - 550 - 602 + 349 = 2092.
So, the ANSWER to (a) is 2092.
(b) This number is the complement of 2092 to 2468, i.e. 2468-2092 = 376.
(e) This set is precisely the union of the three subsets P, D and H.
The number of elements in this union we just calculated in (a): it is 2092.
(F) It is easy. To compute the number of these students, take the number of students in (H U D),
it is 602 (given), and subtract from it the number of student in the triple intersection, which is 349.
So, the difference 602 - 349 = 253 is the ANSWER to (f)
I hope that from my post you will learn a lot of useful information.
-------------------
On inclusion-exclusion principle, see this Wikipedia article
https://en.wikipedia.org/wiki/Inclusion%E2%80%93exclusion_principle
To see many other similar (and different) solved problems, see the lessons
- Counting elements in sub-sets of a given finite set
- Advanced problems on counting elements in sub-sets of a given finite set
- Challenging problems on counting elements in subsets of a given finite set
- Selected problems on counting elements in subsets of a given finite set
- Inclusion-Exclusion principle problems
in this site.
Happy learning (!)
Question 1206205: Given that
U={1,2,3,...,11,12,13}
A={3,5,7,8,9,11}
B= {4,5,6,9,10}
C={1,3,4,5,6,7,10,12}
Determine which elements land in each region of the following Venn Diagram.
ABCI.II.III.IV.V.VI.VII.VIII.
LIST the elements in each of the following regions in set notation: Hint
Region I =
Hint
Region II =
Hint
Region III =
Hint
Region IV =
Hint
Region V =
Hint
Region VI =
Hint
Region VII =
Hint
Region VIII =
Hint
Submit QuestionQuestion 7
Found 2 solutions by math_tutor2020, ikleyn:
Answer by math_tutor2020(3816) (Show Source):
You can put this solution on YOUR website!
I'm not sure if you posted a screenshot, but your diagram isn't showing up.
This is probably what your Venn Diagram looks like
If my assumption is incorrect then please let me know.
U={1,2,3,...,11,12,13} is the universal set
Inside the universal set are these subsets
A={3,5,7,8,9,11}
B= {4,5,6,9,10}
C={1,3,4,5,6,7,10,12}
we have n = 3 subsets and 2^n = 2^3 = 8 distinct regions.
Let's form the following table
| U | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | | A | | | 3 | | 5 | | 7 | 8 | 9 | | 11 | | | | B | | | | 4 | 5 | 6 | | | 9 | 10 | | | | | C | 1 | | 3 | 4 | 5 | 6 | 7 | | | 10 | | 12 | |
The top row represents the universal set.
Then sets A,B,C are the next three rows.
I've spaced things out so that the items line up.
Then go through each column one at a time to sort out the values.
The number "1" is found in set C only.
So we'll write "1" in region VII aka region 7.
This is in circle C and outside the other circles.
The number "2" is not in any of the three sets.
This value is written outside of the circles (region VIII aka region 8).
The number "3" is found in sets A and C, but not in set B.
Write this value in region IV aka region 4.
Keep this process going until you've reached the right-most edge of the table.
This is what you should get when filling out the Venn Diagram
Notice region III has no values in it.
This is because there aren't any values in set B only.
Answer by ikleyn(52778) (Show Source):
You can put this solution on YOUR website! .
In the post, Venn diagram is not shown,
so the information, which is necessary for the solution,
can not be decoded/deciphered from the post.
Question 1206206: A survey was conducted at a local ballroom dance studio asking students what dances they competed in at the most recent competition. Below are the results for the dances Waltz,Bachata, and Mambo:
WaltzBachataMambo278304397205313222217243
a) How many students competed in Waltz, Bachata, or Mambo?
b) How many students competed in Bachata & Mambo, but not Waltz?
c) How many students competed in Waltz or Mambo, but not Bachata?
d) How many students competed in Waltz & Bachata or competed in Bachata & Mambo?
e) How many students competed in none of these three dances?
Answer by ikleyn(52778) (Show Source):
Question 1205816: Among 70 Jambites, a survey shows that: 23 were taking Physics 25 were taking Biology 22 were taking Chemistry 6 were taking Physics and Biology 7 were taking Biology and Chemistry 8 were taking Chemistry and Physics 2 were taking Physics, Biology and chemistry. (a) How many of the Jambites were taking none of the three sciences? (b) How many were taking just one of the three subjects?
Answer by ikleyn(52778) (Show Source):
You can put this solution on YOUR website! .
Among 70 students, a survey shows that:
23 were taking Physics, 25 were taking Biology, 22 were taking Chemistry
6 were taking Physics and Biology, 7 were taking Biology and Chemistry, 8 were taking Chemistry and Physics
2 were taking Physics, Biology and chemistry.
(a) How many of the students were taking none of the three sciences?
(b) How many were taking just one of the three subjects?
~~~~~~~~~~~~~~~~~~~~~~~
You are given the universal set U of 70 students and 3 its basic subsets P, B and C
(see the table below).
U 70 total students
P 23 Physics
B 25 Biology
C 22 Chemistry
Also, you are given info about their in-pair intersections and about their triple intersection.
PB 6 Physics and Biology
BC 7 Biology and Chemistry
PC 8 Chemistry and Physics
PBC 2 Physics, Biology and chemistry
Having this info well organized, you can easily answer all questions (a), and (b).
(a) The set of students not taking any of the three subjects is U \ (P U B U C).
So, calculate the number of students in the union (P U B U C} first.
For it, use the inclusion-exclusion princuple/(formula)
n(P U B U C) = n(P) + n(B) + n(C) - n(PB) - n(BC) - n(PC) + n(PBC) =
= 23 + 25 + 22 - 6 - 7 - 8 + 2 = 51.
Now the next step gives the answer to question (a) :
the number of students taking none of the three sciences = 70 - 51 = 19. ANSWER
(b) The number of students taking Physics only, n(Po), is
n(Po) = n(P) - n(PB) - n(PC) + n(PBC) = 23 - 6 - 8 + 2 = 11.
The number of students taking Biology only, n(Bo), is
n(Bo) = n(B) - n(PB) - n(BC) + n(PBC) = 25 - 6 - 7 + 2 = 14.
The number of students taking Chemistry only, n(Co), is
n(Co) = n(C) - n(PC) - n(BC) + n(PBC) = 22 - 8 - 7 + 2 = 9.
The number of students taking just one of the three subjects is
n(Po) + n(Bo) + n(Co) = 11 + 14 + 9 = 34.
Solved.
----------------
On inclusion-exclusion principle, see this Wikipedia article
https://en.wikipedia.org/wiki/Inclusion%E2%80%93exclusion_principle
To see many other similar (and different) solved problems, see the lessons
- Counting elements in sub-sets of a given finite set
- Advanced problems on counting elements in sub-sets of a given finite set
- Challenging problems on counting elements in subsets of a given finite set
- Selected problems on counting elements in subsets of a given finite set
- Inclusion-Exclusion principle problems
in this site.
Happy learning (!)
Question 1205085: 
Answer by MathLover1(20849)  (Show Source):
You can put this solution on YOUR website!
 = , , , , , , ,
 =, ,, ,, ,,
 =,,, ,,,,
 =,,,,,,,
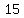
( U )=,,,,,,,,,
( U ) ∩ = , , , , , ,
( U )=, , , , , , , , , , ,
(( U ) ∩ ) U ( U )= ,,,,,,,,,,,,
the sum=
|
Older solutions: 1..45, 46..90, 91..135, 136..180, 181..225, 226..270, 271..315, 316..360, 361..405, 406..450, 451..495, 496..540, 541..585, 586..630, 631..675, 676..720, 721..765, 766..810, 811..855, 856..900, 901..945, 946..990, 991..1035
|
.
