Tutors Answer Your Questions about Numeric Fractions (FREE)
Question 1210392: It costs £11.25 a day to stay in a hotel in
September and £88.25 a week in August.by
comparing the cost of a week holiday in
September with that of a week's holiday in
August find ratio of cost in lowest terms
Answer by ikleyn(52776)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
D U P L I C A T E
Just solved at this forum under this link
https://www.algebra.com/algebra/homework/NumericFractions/Numeric_Fractions.faq.question.1210393.html
Question 1210393: It costs £11.25 a day to stay in a hotel in
September and £88.25 a week in August.by
comparing the cost of a week holiday in
September with that of a week's holiday in
August find ratio of cost in lowest terms
Answer by greenestamps(13198)   (Show Source): (Show Source):
You can put this solution on YOUR website!
Since the problem asks to compare the weekly costs as a ratio in lowest terms, it might be easiest to convert the given decimal costs into fractions. Note this will be relatively easy, because both given rates involve .25 = 1/4 of a pound.
one day in September: 11.25 = 45/4
one week = 7 days in September: 7*(45/4) = 315/4
one week in August: 88.25 = 353/4
The ratio is 315/353. Those whole numbers have no common factor, so that ratio is in lowest terms.
ANSWER: 315/353, or 315:353
Question 1210390: 100 coins are on a table showing 10 heads and 90 tails. You are blindfolded. Is it possible to divide the coins into 2 piles with an equal number of heads?
Found 2 solutions by math_tutor2020, ikleyn:
Answer by math_tutor2020(3816)  (Show Source): (Show Source):
You can put this solution on YOUR website!
Label the piles A and B.
Randomly select 10 coins to form pile A.
The remaining 90 coins are pile B.
Let x be a whole number in the set {0,1,2,...,9,10}
x is between 0 and 10
If x coins in pile A are heads, then 10-x coins in pile A are tails since pile A has 10 coins.
Further we know there are 10-x heads in pile B since there are 10 heads total.
Turn over all coins in pile A.
x heads ---> x tails
10-x tails ---> 10-x heads
We'll have 10-x heads in pile A and 10-x heads in pile B.
At this point we have guaranteed both piles have the same number of heads.
Unfortunately we won't be able to determine how many heads are in each pile.
--------------------------------------------------------------------------
Let's look at an example.
Let's say there are x = 3 heads in pile A and 10-x = 10-3 = 7 tails in pile A.
The remaining 10-x = 10-3 = 7 heads are in pile B.
Now let's turn over every coin in pile A.
3 heads ----> 3 tails
7 tails ----> 7 heads
We will have 7 heads in each pile.
I encourage you to try other values of x in the set {0,1,2,...,9,10} so you can get a sense of how this is working.
Note carefully I say "turn over" rather than "flip" because I want to avoid the idea of randomly flipping a coin.
When I say "turn over" I simply mean "any heads becomes tails or vice versa".
--------------------------------------------------------------------------
Quick Recap: Select any 10 random coins. Turn those 10 coins over (leave the rest as they are).
Answer by ikleyn(52776)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
100 coins are on a table showing 10 heads and 90 tails. You are blindfolded.
Is it possible to divide the coins into 2 piles with an equal number of heads?
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
Yes, of course - if you ask another person, who is sighted, to do it for you :)
Another way for a blindfolded person to perform this assignment on his or on her own
is to select 5 head coins from the entire collection of 100 coins by touch.
In this case, you use your tactile senses instead of your sight.
To me, it remains unclear how this post and your question do relate to Math . . .
Question 1210383: From a ceartain number 3 is subtracted the result is divided by 2 the final answer is 5 find the number
Found 2 solutions by ikleyn, josgarithmetic:
Answer by ikleyn(52776)   (Show Source): (Show Source):
Answer by josgarithmetic(39616)  (Show Source): (Show Source):
Question 1210381: Divide 40 by thn sum of 3 and 5
Answer by greenestamps(13198)   (Show Source): (Show Source):
Question 1210254: Of 90 students who took Biology and Geography test, 5/12 took Biology and 5/6 Geography.
Every candidate took at least one of the two subjects.
i. What fraction of the students took both subjects?
ii. What fraction of the students took Biology but not Geography?
Answer by ikleyn(52776)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
Of 90 students who took Biology and Geography test, 5/12 took Biology and 5/6 Geography.
Every candidate took at least one of the two subjects.
i. What fraction of the students took both subjects?
ii. What fraction of the students took Biology but not Geography?
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
The problem is fatally DEFECTIVE,
since 5/12 of 90 students is 37.5, which is not a whole number.
XXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXX
I posted this "problem" to the Google AI, and Google AI produced incorrect answer
without making a preliminary analysis of the input data for correctness.
See this Google-AI solution of 05/01/2025 under this link
https://www.google.com/search?q=Of+90+students+who+took+Biology+and+Geography+test%2C+5%2F12+took+Biology+and+5%2F6+Geography.+Every+candidate+took+at+least+one+of+the+two+subjects.+i.+What+fraction+of+the+students+took+both+subjects%3F+ii.+What+fraction+of+the+students+took+Biology+but+not+Geography%3F&rlz=1C1CHBF_enUS1071US1071&oq=Of+90+students+who+took+Biology+and+Geography+test%2C+5%2F12+took+Biology+and+5%2F6+Geography.+Every+candidate+took+at+least+one+of+the+two+subjects.+i.+What+fraction+of+the+students+took+both+subjects%3F+ii.+What+fraction+of+the+students+took+Biology+but+not+Geography%3F&gs_lcrp=EgZjaHJvbWUyBggAEEUYOdIBCTI4ODJqMGoxNagCCLACAfEFoNXAzHHOyK7xBaDVwMxxzsiu&sourceid=chrome&ie=UTF-8
Naturally, I posted them my notice saying that their solution was incorrect.
It confirms the basic truth: the AI in its current version works perfectly,
if it finds a source in the Internet to re-write from;
and it is powerless, when it does not find such a source in the Internet to re-write from.
Question 1210168: How do I subtract a whole number from a fraction for example:
5-3/4 and 8 3/5-2 8/9
Thank you for your time regarding these questions.
Answer by josgarithmetic(39616)  (Show Source): (Show Source):
Question 1209939: If m is a positive integer and sqrt(4m^2+29) is an integer, then what is m?
Found 4 solutions by AnlytcPhil, mccravyedwin, ikleyn, math_tutor2020:
Answer by AnlytcPhil(1806)   (Show Source): (Show Source):
You can put this solution on YOUR website!
Tutor Ikleyn states
29 is a prime number, so it has two possible decompositions in the product of
prime numbers
29 = 1* 29 or 29 = (-1)*(-29).
You may not say that. You may say:
29 is a prime number, so it has ONE possible decomposition in the product of
prime numbers
29 = 1* 29.
Or you may say:
29 is a prime number, so it has two possible decompositions in the product of
integers.
29 = 1* 29 or 29 = (-1)*(-29).
Edwin
Answer by mccravyedwin(406)   (Show Source): (Show Source):
You can put this solution on YOUR website!
Tutor Ikleyn states
29 is a prime number, so it has two possible decompositions in the product of
prime numbers
29 = 1* 29 or 29 = (-1)*(-29).
But unless we are in modern algebra where there are such things as "groups",
"rings", etc., and where "prime number" has a different definition, then "prime
number" always means a positive integer with exactly 2 unique positive integer
factors.
While 29 = (-1)*(-29) is true, it is not a decomposition in the product of prime
numbers.
Edwin
Answer by ikleyn(52776)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
If m is a positive integer and sqrt(4m^2+29) is an integer, then what is m?
~~~~~~~~~~~~~~~~~~~~~~~~~
If 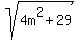 is an integer number n, then
4m^2 + 29 = n^2
29 = n^2 - 4m^2
29 = (n-2m)*(n+2m).
29 is a prime number, so it has two possible decompositions into the product of prime factors
29 = 1* 29 or 29 = (-1)*(-29).
Therefore, we have 4 systems of linear equations to analyze
n - 2m = 1, (1)
n + 2m = 29, (2)
n - 2m = -1, (3)
n + 2m = -29, (4)
n - 2m = 29, (5)
n + 2m = 1, (6)
n - 2m = -29, (7)
n + 2m = -1. (8)
From system (1), (2), by subtracting equations, we have
2m - (-2m) = 29-1, 4m = 28, m = 28/4 = 7 and then n = 1 + 2m = 1 + 2*7 = 15.
So, the solution pair is (m,n) = (7,15), and it works properly: is an integer number n, then
4m^2 + 29 = n^2
29 = n^2 - 4m^2
29 = (n-2m)*(n+2m).
29 is a prime number, so it has two possible decompositions into the product of prime factors
29 = 1* 29 or 29 = (-1)*(-29).
Therefore, we have 4 systems of linear equations to analyze
n - 2m = 1, (1)
n + 2m = 29, (2)
n - 2m = -1, (3)
n + 2m = -29, (4)
n - 2m = 29, (5)
n + 2m = 1, (6)
n - 2m = -29, (7)
n + 2m = -1. (8)
From system (1), (2), by subtracting equations, we have
2m - (-2m) = 29-1, 4m = 28, m = 28/4 = 7 and then n = 1 + 2m = 1 + 2*7 = 15.
So, the solution pair is (m,n) = (7,15), and it works properly:
 = = 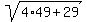 = = 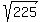 = 15.
From system (3), (4), by subtracting equations, we have
2m - (-2m) = -29-(-1), 4m = -28, m = -28/4 = -7.
It does not work, since the number m should be positive, by the condition.
From system (5), (6), by subtracting equations, we have
2m - (-2m) = 1-29, 4m = -28, m = -28/4 = -7.
It does not work, since the number m should be positive, by the condition.
From system (7), (8), by subtracting equations, we have
2m - (-2m) = -1 - (-29), 4m = 28, m = 28/4 = 7 and then n = 1 + 2m = 1 + 2*7 = 15.
So, the solution pair is (m,n) = (7,15), the same as we got from system (1), (2),
and it works properly: = 15.
From system (3), (4), by subtracting equations, we have
2m - (-2m) = -29-(-1), 4m = -28, m = -28/4 = -7.
It does not work, since the number m should be positive, by the condition.
From system (5), (6), by subtracting equations, we have
2m - (-2m) = 1-29, 4m = -28, m = -28/4 = -7.
It does not work, since the number m should be positive, by the condition.
From system (7), (8), by subtracting equations, we have
2m - (-2m) = -1 - (-29), 4m = 28, m = 28/4 = 7 and then n = 1 + 2m = 1 + 2*7 = 15.
So, the solution pair is (m,n) = (7,15), the same as we got from system (1), (2),
and it works properly:  = = 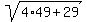 = = 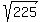 = 15.
ANSWER. For the given problem, there is a unique solution for m. It is m = 7. = 15.
ANSWER. For the given problem, there is a unique solution for m. It is m = 7.
Solved.
I placed this my solution here after the solution by tutor @math_tutor2020 to make the analysis complete.
///////////////////////////
My comment/response to the Edwin's comment, regarding my post.
For this given problem, considering all four decompositions
29 = 1*29 = 29*1 = (-1)*(-29) = (-29)*(-1)
is NECESSARY for the completeness of the analysis.
So, all 4 (four) cases/decompositions MUST be considered, exactly as it was made in my post.
Answer by math_tutor2020(3816)  (Show Source): (Show Source):
You can put this solution on YOUR website!
Answer: m = 7
Work Shown
k = some integer
k = sqrt(4m^2+29)
k^2 = 4m^2+29
k^2-4m^2 = 29
(k-2m)(k+2m) = 29
29 is prime so the only factors are 1 and 29.
k and m are integers, so k-2m and k+2m are also integers.
In order for (k-2m)(k+2m) = 29 to be the case, we'd need either

or

In either system of equations, adding straight down leads to 2k = 30 which solves to k = 15.
Then,
k-2m = 1
15-2m = 1
-2m = 1-15
-2m = -14
m = -14/(-2)
m = 7
Or,
k-2m = 29
15-2m = 29
-2m = 29-15
-2m = 14
m = 14/(-2)
m = -7
We ignore m = -7 since your teacher stated that m > 0
Check: sqrt(4m^2+29)=sqrt(4*7^2+29)=15 is an integer.
Question 1209894: 1). 4 is 2/5 of what number?
2). 4 is 1/3 of what number?
These are questions in the book that I need to explain to the students.
Found 3 solutions by math_tutor2020, timofer, ikleyn:
Answer by math_tutor2020(3816)  (Show Source): (Show Source):
You can put this solution on YOUR website!
I'll do the first question to get you started.
x = some unknown number
(2/5)x = two fifths of that number, "of" means "multiply"
4 = (2/5)x
5*4 = 2x
20 = 2x
x = 20/2
x = 10
4 is 2/5 of 10
As a check,
(2/5)x = (2/5)*10 = (2*10)/5 = 20/5 = 4
The answer is confirmed.
Answer by timofer(104)  (Show Source): (Show Source):
Answer by ikleyn(52776)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
(1) 4 is 2/5 of what number ?
If 4 is 2/5 of some number, then 1/5 of that number is half of 4, i.e. 4/2 = 2.
Next, since 2 is 1/5 of the number, then the whole number is 5 times 2, i.e.10.
ANSWER. 4 is 2/5 of 10.
(2) 4 is 1/3 of what number ?
If 4 is 1/3 of some number, then that whole number is 3 times 4, i.e. 3*4 = 12.
ANSWER. 4 is 1/3 of 12.
Solved, with explanations.
Question 1171310: Use a graphing utility to create a scatter diagram of the data given in the table. Observe the shape of the scatter diagram to determine whether the data is best described by an exponential, logarithmic, or logistic model. Then use the appropriate regression feature to find an equation that models the data. When necessary, round values to five decimal places.
x 1 2 3 4 5 6 7 8 9 10
f(x) 409.6 260.4 170.3 110.9 74.1 44.4 32.5 19.2 12.8 8.4
Answer by CPhill(1959)   (Show Source): (Show Source):
You can put this solution on YOUR website! Absolutely! Let's analyze the data and find the appropriate model.
**1. Create the Scatter Diagram:**
The scatter diagram will help us visualize the relationship between x and f(x).
```python
import matplotlib.pyplot as plt
import numpy as np
x = [1, 2, 3, 4, 5, 6, 7, 8, 9, 10]
f_x = [409.6, 260.4, 170.3, 110.9, 74.1, 44.4, 32.5, 19.2, 12.8, 8.4]
plt.scatter(x, f_x)
plt.xlabel('x')
plt.ylabel('f(x)')
plt.title('Scatter Diagram')
plt.grid(True)
plt.show()
```
**2. Observe the Shape:**
The scatter plot shows a decreasing trend, where the rate of decrease slows down as x increases. This suggests an **exponential decay** model.
**3. Find the Exponential Model:**
We will use the exponential regression feature to find the equation that best fits the data.
An exponential model has the form: f(x) = a * e^(-bx)
```python
from scipy.optimize import curve_fit
def exponential_func(x, a, b):
return a * np.exp(-b * x)
popt, pcov = curve_fit(exponential_func, x, f_x)
a_fit = popt[0]
b_fit = popt[1]
print(f"Exponential Model: f(x) = {a_fit:.5f} * e^(-{b_fit:.5f} * x)")
```
**Output:**
Exponential Model: f(x) = 630.48226 * e^(-0.43561 * x)
**4. Conclusion:**
The data is best described by an exponential decay model. The equation that models the data is:
f(x) = 630.48226 * e^(-0.43561 * x)
Question 1209811: Find the sum
\frac{1}{7} + \frac{2}{7^2} + \frac{3}{7^3} + \frac{1}{7^4} + \frac{2}{7^5} + \frac{3}{7^6}
Answer by CPhill(1959)   (Show Source): (Show Source):
You can put this solution on YOUR website! Let $S = \frac{1}{7} + \frac{2}{7^2} + \frac{3}{7^3} + \frac{1}{7^4} + \frac{2}{7^5} + \frac{3}{7^6}$.
We can group the terms in sets of three:
$S = \left(\frac{1}{7} + \frac{2}{7^2} + \frac{3}{7^3}\right) + \left(\frac{1}{7^4} + \frac{2}{7^5} + \frac{3}{7^6}\right)$.
Let $A = \frac{1}{7} + \frac{2}{7^2} + \frac{3}{7^3}$.
Then $S = A + \frac{1}{7^3} A = A\left(1 + \frac{1}{7^3}\right)$.
We have $A = \frac{1}{7} + \frac{2}{49} + \frac{3}{343} = \frac{49}{343} + \frac{14}{343} + \frac{3}{343} = \frac{49+14+3}{343} = \frac{66}{343}$.
Then $S = \frac{66}{343}\left(1 + \frac{1}{343}\right) = \frac{66}{343}\left(\frac{343+1}{343}\right) = \frac{66}{343}\left(\frac{344}{343}\right) = \frac{66\cdot 344}{343\cdot 343} = \frac{22704}{117649}$.
We can also write
$S = \sum_{k=0}^1 \left( \frac{1}{7^{3k+1}} + \frac{2}{7^{3k+2}} + \frac{3}{7^{3k+3}} \right) = \sum_{k=0}^1 \frac{1 \cdot 7^2 + 2 \cdot 7 + 3}{7^{3k+3}} = \sum_{k=0}^1 \frac{49+14+3}{7^{3k+3}} = \sum_{k=0}^1 \frac{66}{7^{3k+3}}$.
$S = \frac{66}{7^3} + \frac{66}{7^6} = \frac{66}{343} + \frac{66}{117649} = \frac{66\cdot 343 + 66}{117649} = \frac{66(343+1)}{117649} = \frac{66(344)}{117649} = \frac{22704}{117649}$.
Final Answer: The final answer is $\boxed{\frac{22704}{117649}}$
Question 1191696: 2. Then grade point averages of 20 college students selected at random from the graduating class are as follows:
3.2 1.9 2.7 2.4
2.8 2.9 3.8 3.0
2.5 3.3 1.8 2.5
3.7 2.8 2.0 3.2
2.3 2.1 2.5 1.9
a. Calculate the descriptive statistics.
b. Use the appropriate graph for the GPA of the 20 students.
Answer by CPhill(1959)   (Show Source): (Show Source):
You can put this solution on YOUR website! Here's the solution:
**a. Descriptive Statistics**
First, let's organize the data in ascending order to make calculations easier:
1.8, 1.9, 1.9, 2.0, 2.1, 2.3, 2.4, 2.5, 2.5, 2.5, 2.7, 2.8, 2.8, 2.9, 3.0, 3.2, 3.2, 3.3, 3.7, 3.8
Now we can calculate the descriptive statistics:
* **Mean:** (Sum of all values) / (Number of values)
Mean = (1.8 + 1.9 + 1.9 + 2.0 + 2.1 + 2.3 + 2.4 + 2.5 + 2.5 + 2.5 + 2.7 + 2.8 + 2.8 + 2.9 + 3.0 + 3.2 + 3.2 + 3.3 + 3.7 + 3.8) / 20
Mean = 51.5 / 20 = 2.575
* **Median:** The middle value (since there are 20 values, the median is the average of the 10th and 11th values)
Median = (2.5 + 2.7) / 2 = 2.6
* **Mode:** The most frequent value(s)
Mode = 2.5 (appears 3 times)
* **Range:** Maximum value - Minimum value
Range = 3.8 - 1.8 = 2.0
* **Variance:** The average of the squared differences from the mean. Here's how to calculate it:
1. Subtract the mean from each value and square the result.
2. Sum all the squared differences.
3. Divide the sum by the number of values minus 1 (n-1 = 20-1 =19 for sample variance). This is called the sample variance.
Variance ≈ 0.355 (You can use a calculator or spreadsheet software for this).
* **Standard Deviation:** The square root of the variance
Standard Deviation ≈ √0.355 ≈ 0.596
**b. Appropriate Graph**
A **histogram** or a **stem-and-leaf plot** would be appropriate for visualizing the GPA data. A histogram is generally preferred for larger datasets. Here's what a histogram would look like conceptually:
* **X-axis:** GPA ranges (e.g., 1.8-2.0, 2.0-2.2, 2.2-2.4, ..., 3.8-4.0)
* **Y-axis:** Frequency (number of students in each GPA range)
You would then create bars for each GPA range, with the height of the bar representing the number of students whose GPAs fall within that range.
A stem-and-leaf plot would also be suitable, especially since the dataset is relatively small. It would show the individual data points while still giving a sense of the distribution. Here's how it would look:
```
1 | 899
2 | 01345557889
3 | 022378
```
Where the "stem" is the digit before the decimal point, and the "leaves" are the digits after the decimal point.
Both the histogram and stem-and-leaf plot would give you a visual representation of the distribution of GPAs among the 20 students.
Question 1209393: Compute
1/(1*4) + 1/(4*7) + 1/(7*12)
Answer by ikleyn(52776)   (Show Source): (Show Source):
Question 1209284: which of the following numbers is the smallest? A. 3/7 B.1/3 C.5/6 D.9/14
Found 3 solutions by math_tutor2020, mccravyedwin, ikleyn:
Answer by math_tutor2020(3816)  (Show Source): (Show Source):
You can put this solution on YOUR website! Answer: 1/3
Explanation
The other tutors have great responses.
I'll offer another approach.
Let's compare the fractions A and B
For now assume they are equal.
We can use the cross multiplication rule like so
3/7 = 1/3
3*3 = 7*1
9 = 7
The last equation is false since the two sides don't agree on the same number.
To fix the error, change each equal sign to a greater than sign.
3/7 > 1/3
3*3 > 7*1
9 > 7
We determine that 3/7 is larger than 1/3.
Cross choice A off the list.
So far 1/3 is the smallest value.
But there could be another fraction in this list that's smaller.
Now let's compare B and C.
Like before we assume they are equal, and use the cross multiplication rule to get,
1/3 = 5/6
1*6 = 3*5
6 = 15
This is false, so let's fix the errors.
1/3 < 5/6
1*6 < 3*5
6 < 15
The fraction 1/3 is still the smallest so far.
Cross choice C off the list.
The last comparison is to look at B and D.
1/3 = 9/14
1*14 = 3*9
14 = 27
Let's fix the errors
1/3 < 9/14
1*14 < 3*9
14 < 27
Cross choice D off the list since D is larger than B.
Therefore 1/3 is the smallest fraction in the list.
Answer by mccravyedwin(406)   (Show Source): (Show Source):
You can put this solution on YOUR website!
An alternate way, if you are allowed to use a calculator,
such as when you're at home, and want to check your answer to
see if they're correct.
Just get a calculator, divide them out and line up the decimal points:
A. 3/7 = 3÷7 = 0.4285714286...
B. 1/3 = 1÷3 = 0.3333333333...
C. 5/6 = 5÷6 = 0.8333333333...
D. 9/14 = 9÷14 = 0.6428571429...
Look at the column of first digits. They're all the same, 0, so you can't tell.
Look at the 2nd digits, (the first ones after the decimal). They are 4,3,8,6.
That's all you need. 3 is the smallest, so 1/3 is the smallest.
If the column of first digits are all the same, you go to the column of second
digits and pick the smallest. If the second digits are all the same, you go to
the column of third digits and pick the smallest, etc., etc.
----------------------------------------------------------------------
Suppose you were given this problem to find the smallest:
A. 37/140 B. 183/700 C. 46/175 D. 939/3500
A. 37/140 = 37÷140 = 0.2642857143...
B. 183/700 = 183÷700 = 0.2614286714...
C. 46/175 = 46÷175 = 0.2628571429...
D. 939/3500 = 939÷3500 = 0.2682857143...
You would have to go to the column of 4th digits (3rd digits after the decimal),
4,1,2,8 to see that the smallest would be 183/700.
Edwin
Answer by ikleyn(52776)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
which of the following numbers is the smallest? A. 3/7 B.1/3 C.5/6 D.9/14
~~~~~~~~~~~~~~~~~~~~~~~~~~
Write these numbers with the common denominator.
The Least Common Denominator (LCD) is 7*3*2 = 42.
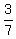 = = 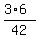 = = 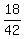 . .
 = = 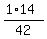 = = 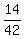 . .
 = = 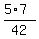 = = 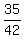 . .
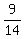 = = 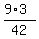 = = 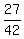 .
Comparing fractions (their numerators), you see that .
Comparing fractions (their numerators), you see that 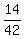 is the smallest number.
ANSWER. is the smallest number.
ANSWER. 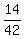 = =  is the smallest number. is the smallest number.
Solved.
---------------------
There are other, even more effective ways to find the smallest number.
For example, 1/3 multiplied by 3 gives 1.
All other listed numbers, multiplied by 3, give the product greater than 1 (which is OBVIOUS).
It means that 1/3 is the smallest number among the listed.
Nevertheless, the explanation, which I gave in first part of my post, is the #1 explanation
to this question, which a teacher usually provides to students in the class at normal study process.
All other explanations are #2, #3, #4 and so on . . .
Question 1209283: If 1/a + 1/b = 5/12 and ab = 24, what is the value of a+b?
Answer by math_tutor2020(3816)  (Show Source): (Show Source):
Question 1209253: Evaluate 4 to the 5/2
Found 2 solutions by math_tutor2020, ikleyn:
Answer by math_tutor2020(3816)  (Show Source): (Show Source):
You can put this solution on YOUR website!
Your question could be interpreted as either 4^(5/2) or (4^5)/2
The 1st case has "5/2" as the exponent.
The 2nd case is all of "4^5" over top 2.
If we go with the 1st option, then,
4^(5/2)
= ( 4^(1/2) )^5
= ( sqrt(4) )^5
= ( 2 )^5
= 32
Or, if it's the 2nd option,
(4^5)/2
= (1024)/2
= 512
Answer by ikleyn(52776)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
Unclear.
To me, it is unclear what you want.
The wording in your post is ambiguous.
////////////////////
In addition to interpretation by the other tutor, it can be interpreted as 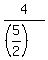 . .
Using words instead of formulas in Math almost always leads to ambiguity.
It is why special mathematical language was developed 200 - 300 years ago
to use it in Math, which never produces ambiguity.
Using right accurate language in Math is a form of respectful communication in Math.
It is MUST.
Using wrong inaccurate language in Math of the type " bla-bla-bla " is a form
of disrespectful communication in Math.
Learn and memorize.
Question 1209224: If 2x-3y = 5, then find (9^x)/(27^y) = ??
Answer by math_tutor2020(3816)  (Show Source): (Show Source):
You can put this solution on YOUR website!
Answer: 243
Work Shown
(9^x)/(27^y)
= ((3^2)^x)/((3^3)^y)
= (3^(2x))/(3^(3y))
= 3^(2x-3y)
= 3^(5)
= 243
We conclude that (9^x)/(27^y) = 243 when 2x-3y = 5.
--------------------------------------------------------------------------
Another approach.
Pick any point on the line 2x-3y = 5.
Let's say we pick the point (x,y) = (4,1).
You can determine this point by looking at the graph, or do a bit of trial-and-error.
Note that 2x-3y = 2*4-3*1 = 8-3 = 5 which confirms (4,1) is on this line.
This ordered pair makes 2x-3y = 5 true.
(9^x)/(27^y)
= (9^4)/(27^1)
= (6561)/(27)
= 243
We arrive at the same answer.
Question 1209050: Frank spent 1/7 of his money on shoes and 2/5 of the remaining amount on a shirt. How much money does he have left in terms of a fraction of the original amount?
Found 3 solutions by MathTherapy, math_tutor2020, ikleyn:
Answer by MathTherapy(10551)   (Show Source): (Show Source):
Answer by math_tutor2020(3816)  (Show Source): (Show Source):
You can put this solution on YOUR website!
Answer: 18/35
Explanation
Draw a grid of rectangles that are 7 units tall and 5 units across.

You can use graph paper or make your own grid.
Another approach is to take a screenshot of a blank excel spreadsheet so you can use it in something like MS Paint.
Shade the entire top row to represent Frank spending 1/7 of his starting money. You have shaded 1 row out of 7 rows total. The unshaded stuff is what he has left after buying the shoes (but he hasn't bought the shirt just yet). I'll represent this shading with a red X.
Then shade two entire columns (out of the 5 total columns) so we can depict Frank spending 2/5 of his remaining money. I'll represent this additional shading with a blue X. The unshaded blocks represent his remaining amount of money after buying the shoes and shirt.

The final unshaded region is 6 units tall and 3 units across.
There are 6*3 = 18 small rectangles in this unshaded region.
This is out of 7*5 = 35 original small rectangles.
18/35 is the final answer. The fraction cannot be reduced since 18 and 35 do not have any common factors other than 1.
----------------------------------------
A non-visual method.
Frank spends 1/7 his money on shoes.
He has 1 - (1/7) = 6/7 of it remaining after buying the shoes.
Since he spends 2/5 of that on a shirt, he keeps 3/5 of that leftover portion.
(6/7)*(3/5) = (6*3)/(7*5) = 18/35
----------------------------------------
An example
Let's say Frank starts with $350.
He spends (1/7)*350 = 50 dollars on shoes.
After buying the shoes, he would have 350-50 = 300 dollars.
(2/5)*300 = 120 dollars is spent on the shirt and his final leftover amount is 300-120 = 180 dollars.
Then 180/350 = (18*10)/(35*10) = 18/35 is the fractional amount he has compared to the starting $350.
18/35 = 0.51429 = 51.429% approximately
Answer by ikleyn(52776)   (Show Source): (Show Source):
Question 1209034: Fill in the blank to make the equation true.
8/125*___ = 5/2
Found 2 solutions by MathTherapy, greenestamps:
Answer by MathTherapy(10551)   (Show Source): (Show Source):
You can put this solution on YOUR website!
Fill in the blank to make the equation true.
8/125*___ = 5/2
An EXAMPLE: 5 * ___ = 10
Obviously the blank, "___" is obtained by DIVIDING 10 by 5, which is 2.
Apply the same concept to this problem.
8/125 *___ = 5/2
Obviously the blank, "___" is obtained by DIVIDING 5/2 by 8/125, which is: 
Answer by greenestamps(13198)   (Show Source): (Show Source):
Question 1209190: solve the simultaneous Equations 3a^2 - 4y = -1, 2a - y = 1
Found 2 solutions by timofer, ikleyn:
Answer by timofer(104)  (Show Source): (Show Source):
Answer by ikleyn(52776)   (Show Source): (Show Source):
Question 1208935: True or false? If a and b are both irrational then a*b must always be irrational?
Found 3 solutions by greenestamps, ikleyn, math_tutor2020:
Answer by greenestamps(13198)   (Show Source): (Show Source):
You can put this solution on YOUR website!
FALSE
Let a and b both be equal to the same irrational number of the form 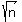 , where n is any positive number. Then , where n is any positive number. Then  , which is rational. , which is rational.
Answer by ikleyn(52776)   (Show Source): (Show Source):
Answer by math_tutor2020(3816)  (Show Source): (Show Source):
Question 1208936: True or false? The sum of rational and irrational number is rational
Answer by math_tutor2020(3816)  (Show Source): (Show Source):
You can put this solution on YOUR website!
Answer: False
Explanation
x = rational number
y = irrational number
x = a/b for some integers a,b where b is nonzero
y cannot be written as a fraction of integers because it is set up to be irrational.
Assume x+y was rational.
We'll do a proof by contradiction to show that x+y is instead irrational.
x+y = rational
x+y = p/q
(a/b) + y = p/q
y = (p/q) - (a/b)
y = (bp)/(bq) - (aq)/(bq)
y = (bp-aq)/(bq)
y = (some integer)/(some integer)
y = rational number
But wait, we made y irrational and now it's rational.
This is clearly a contradiction.
A number cannot be both rational and irrational at the same time.
The term "irrational" literally means "not rational".
This contradiction means the assumption x+y = rational is false, so x+y = irrational must be the case.
A template to write down in your notes would be rational + irrational = irrational
Question 1208933: I'm trying to help my niece. How can I show 1/3+1/4 as a diagram? Thanks!
Found 2 solutions by math_tutor2020, ikleyn:
Answer by math_tutor2020(3816)  (Show Source): (Show Source):
You can put this solution on YOUR website!
Tutor ikleyn's approach of using a watch dial (i.e. analog clock face) is clever. And perhaps the best way to solve this type of problem. This assumes that schools are still teaching students how to read analog clocks in an era of increasing reliance on digital clocks instead.
One thing to point out about her solution is that 35/60 = (7*5)/(12*5) = 7/12.
Just in case if the person asking the question is wondering why 35 minutes is 7/12 of an hour.
Or you can look at it like this:
1/3 of an hour = (1/3)*60 = 20 minutes which represents the "4" on the clock
1/4 of an hour = (1/4)*60 = 15 minutes which represents the "3" on the clock
Adding the clock face values gives 4+3 = 7
There are 12 values on the clock face, so it yields 7/12.
--------------------------------------------------------------------------
If your niece's teacher requires the use of round pizzas or pies for the fraction diagram, then it could look like this:

The portion in blue represents 1/3 aka 4/12.
To go from 1/3 to 4/12, multiply top and bottom by 4.
Notice each third is split into 4 pieces to get 3*4 = 12 pieces total.
What's so special about 12? It's the LCM of 3 and 4.
The yellow portion is 1/4 = 3/12.
Multiply top and bottom by 3.
Each original quarter piece is split 3 ways.
Once everything is in a common denominator (12), we can add the fractions.
Add the numerators only. Leave the denominator as 12.
1/3 + 1/4 = 4/12 + 3/12 = (4+3)/12 = 7/12
In other words,
4 blue + 3 yellow = 7 shaded pieces out of 12 total, that leads to 7/12
You can think of it like 4 pieces + 3 pieces = 7 pieces, where you'd replace each copy of "pieces" with "/12" or "twelfths".
I apologize if the diagram seems a bit cluttered.
There might be a more efficient way of displaying this.
--------------------------------------------------------------------------
Another approach is to use a fraction tape diagram.
Compared to the previous method, I prefer this method better.
This is because it's easier (for me at least) to draw rectangles than to divide up a circle equally.
Here is what the diagram could look like.

The 1st row represents 1/3.
The 2nd row has us rewrite 1/3 as 4/12. Notice the vertical alignment matches perfectly to help visualize 1/3 = 4/12. Put another way: The blue 1/3 in the top row is split into 4 equal smaller pieces, and the same is done to the other unshaded pieces in the top row.
The 3rd row represents the fraction 1/4.
The 4th row has us rewriting 1/4 as 3/12.
The last row of the diagram has us adding the blue smaller pieces and yellow smaller pieces (blues from row 2, yellows from row 4).
This addition is valid because we have a common denominator (12). The color coding is the same as the previous diagram.
Answer by ikleyn(52776)   (Show Source): (Show Source):
Question 1208610: When expanded as a decimal, the fraction $\frac{1}{7}$ has a repetend (the repeating part of the decimal) of $142857$. The last three digits of the repetend are $857$.
When expanded as a decimal, the fraction $\frac{1}{13}$ has a repetend that is $6$ digits long. If the last three digits of the repetend are $ABC$, compute the digits $A$, $B$, and $C$.
Found 2 solutions by math_tutor2020, ikleyn:
Answer by math_tutor2020(3816)  (Show Source): (Show Source):
You can put this solution on YOUR website!
You would use long division to divide 1 over 13.
13 goes out to the left, while 1 goes under the bar.
Here is a calculator that provides a step-by-step walkthrough
https://www.calculatorsoup.com/calculators/math/longdivisiondecimals.php
Adjust the drop-down menu for "decimal places" to 7 or larger.
The calculator will say that
1/13 = 0.076923076923076923... where "076923" repeats forever
The color coding is there to show when one block stops and the next begins.
The repetend is 076923
The last 3 digits are 9, 2, and 3.
A = 9
B = 2
C = 3
Answer by ikleyn(52776)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
Since the method of solution is not predefined in the problem, choose the simplest way making long division of integer numbers.
Doing this way, find the 6-digit repetend, which is 076923.
So, the digits A, B and C are 9, 2, 3, respectively.
Solved (by the simplest way).
Question 1208323: Cam put 4 12/25 pounds of rice in bags that each weigh 7/25 pound. She uses
1/8 of the bags of rice. How many bags of rice are left?
A)2
B)4
C)8
D)14
Found 3 solutions by MathTherapy, ikleyn, greenestamps:
Answer by MathTherapy(10551)   (Show Source): (Show Source):
Answer by ikleyn(52776)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
Cam put 4 12/25 pounds of rice in bags so that each bag  weights 7/25 of a pound. weights 7/25 of a pound.
She uses 1/8 of the bags of rice. How many bags of rice are left?
~~~~~~~~~~~~~~~~~~~~~~~~~~
As a Math problem, the formulation is far from to be perfect and smooth.
Personally to me, this formulation makes me shudder.
Here is much better formulation.
Cam distributes 4 12/25 pounds of rice in small bags evenly so that each bag weighs 7/25 of a pound.
She uses 1/8 of the bags of rice. How many bags of rice are left?
Answer by greenestamps(13198)   (Show Source): (Show Source):
You can put this solution on YOUR website!
pounds of rice: 4 12/25 = 100/25 + 12/25 = 112/25
pounds of rice in each bag: 7/25
Number of bags: (112/25)/(7/25) = 112/7 = 16
Number of bags used: (1/8)(16) = 2
Number of bags left: 16-2 = 14
ANSWER: 14
|
Older solutions: 1..45, 46..90, 91..135, 136..180, 181..225, 226..270, 271..315, 316..360, 361..405, 406..450, 451..495, 496..540, 541..585, 586..630, 631..675, 676..720, 721..765, 766..810, 811..855, 856..900, 901..945, 946..990, 991..1035, 1036..1080, 1081..1125, 1126..1170, 1171..1215, 1216..1260, 1261..1305, 1306..1350, 1351..1395, 1396..1440, 1441..1485, 1486..1530, 1531..1575, 1576..1620, 1621..1665, 1666..1710, 1711..1755, 1756..1800, 1801..1845, 1846..1890, 1891..1935, 1936..1980, 1981..2025, 2026..2070, 2071..2115, 2116..2160, 2161..2205, 2206..2250, 2251..2295, 2296..2340, 2341..2385, 2386..2430, 2431..2475, 2476..2520, 2521..2565, 2566..2610, 2611..2655, 2656..2700, 2701..2745, 2746..2790, 2791..2835, 2836..2880, 2881..2925, 2926..2970, 2971..3015, 3016..3060, 3061..3105, 3106..3150, 3151..3195, 3196..3240, 3241..3285, 3286..3330, 3331..3375, 3376..3420, 3421..3465, 3466..3510, 3511..3555, 3556..3600, 3601..3645, 3646..3690, 3691..3735, 3736..3780, 3781..3825, 3826..3870, 3871..3915, 3916..3960, 3961..4005, 4006..4050, 4051..4095, 4096..4140, 4141..4185, 4186..4230, 4231..4275, 4276..4320, 4321..4365, 4366..4410, 4411..4455, 4456..4500, 4501..4545, 4546..4590, 4591..4635, 4636..4680, 4681..4725, 4726..4770, 4771..4815, 4816..4860, 4861..4905, 4906..4950, 4951..4995, 4996..5040, 5041..5085, 5086..5130, 5131..5175, 5176..5220, 5221..5265, 5266..5310, 5311..5355, 5356..5400, 5401..5445, 5446..5490, 5491..5535, 5536..5580, 5581..5625, 5626..5670, 5671..5715, 5716..5760, 5761..5805, 5806..5850, 5851..5895, 5896..5940, 5941..5985, 5986..6030, 6031..6075, 6076..6120, 6121..6165, 6166..6210, 6211..6255, 6256..6300, 6301..6345, 6346..6390, 6391..6435, 6436..6480, 6481..6525, 6526..6570, 6571..6615, 6616..6660, 6661..6705, 6706..6750, 6751..6795, 6796..6840, 6841..6885, 6886..6930, 6931..6975, 6976..7020, 7021..7065, 7066..7110, 7111..7155, 7156..7200, 7201..7245, 7246..7290, 7291..7335, 7336..7380, 7381..7425, 7426..7470, 7471..7515, 7516..7560, 7561..7605, 7606..7650, 7651..7695, 7696..7740, 7741..7785, 7786..7830, 7831..7875, 7876..7920, 7921..7965, 7966..8010, 8011..8055, 8056..8100, 8101..8145, 8146..8190, 8191..8235, 8236..8280, 8281..8325, 8326..8370, 8371..8415, 8416..8460, 8461..8505, 8506..8550, 8551..8595, 8596..8640, 8641..8685, 8686..8730, 8731..8775, 8776..8820, 8821..8865, 8866..8910, 8911..8955, 8956..9000, 9001..9045, 9046..9090, 9091..9135, 9136..9180, 9181..9225, 9226..9270, 9271..9315, 9316..9360, 9361..9405, 9406..9450, 9451..9495, 9496..9540, 9541..9585, 9586..9630, 9631..9675, 9676..9720, 9721..9765, 9766..9810, 9811..9855, 9856..9900
|






