A rational number is any number that can be expressed exactly as a fraction
of the form 
.
Remember that the word "RATIONAL" is contained in the word "fractional",
(fRAcTIONAL".
That is not to say that a rational number is always expressed as such a
fraction, though, for it may be expressed other ways.
If it is a whole number, it will be expressed that way as 1, 0, -7, 19, etc.
But they are rational numbers because they can all be placed over 1. So all
whole numbers, positive and negative, are rational numbers.
A decimal such as 3.14 is a rational number, for it can be changed to the
rational number form. For example 
.
However the number 
is NOT a rational number. That's because the decimal
form of is not 3.14 exactly, although 3.14 is often used as an
approximation for , but it is only accurate to two decimal places.
is also approximated by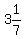 
or 
but does
not equal that. 
Notice that that decimal repeats a block of digits "142857" over and over.
That proves it is a rational number.
7/16 = 0.4375 (the decimal ends(terminates).
1/3 = .33333333333333... (the decimal does not terminate but it repeats 3
over and over forever.
= 2.0768686868686... the decimal repeats "68" over and over
starting with the 3rd decimal place.
Any decimal that stops or repeats a block of digits over and over forever is
a rational number.
So.
1. Any whole number is a rational number.
2. Any common fraction, proper or improper, or mixed fraction, with whole
numbers on top and bottom, is a rational number.
3. Any decimal that terminates is a rational number.
4. Any decimal that repeats a digitit or block of digits forever is a rational
number.
Then what is an irrational number? It is a decimal that never ends, goes on
forever but does not repeat any block of digits forever. Here are some
irrational numbers:
, it never repeats any block of digits forever.
, it never repeats any block of digits forever.
, it never repeats any block of digits forever.
, it never repeats any block of digits forever.
Edwin
