.
Find the remainder when 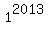 +
+ 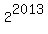 +
+ 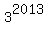 + . . . +
+ . . . +  is divided by 2013.
is divided by 2013.
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
Let's group the addends in pairs
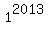 +
+ 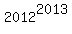 ,
,
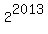 +
+ 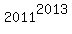 ,
,
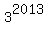 +
+ 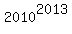 ,
. . . . . . . . . . . .
,
. . . . . . . . . . . .
 +
+ 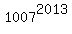 .
Thus, all the addends in the long sum are grouped in pairs this way.
Now use the theorem (= the statement) that for all integers 'a' and 'b' and odd positive integer 'n'
the sum
.
Thus, all the addends in the long sum are grouped in pairs this way.
Now use the theorem (= the statement) that for all integers 'a' and 'b' and odd positive integer 'n'
the sum  +
+ 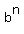 is a multiple of (a+b), so the sum
is a multiple of (a+b), so the sum  +
+ 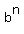 is divisible by (a+b) with zero remainder.
It follows from well known polynomial decomposition
is divisible by (a+b) with zero remainder.
It follows from well known polynomial decomposition
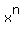 +
+ 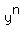 =
= 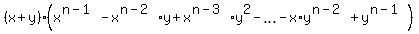 ,
which works for all odd integer 'n'.
Now apply this theorem to each pair formed above.
Since for each pair the sum of integers, that are the bases, is 2013, each and every pair is a multiple of 2013.
Hence, the entire sum of these pairs is a multiple of 2013.
It implies that long sum
,
which works for all odd integer 'n'.
Now apply this theorem to each pair formed above.
Since for each pair the sum of integers, that are the bases, is 2013, each and every pair is a multiple of 2013.
Hence, the entire sum of these pairs is a multiple of 2013.
It implies that long sum 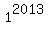 +
+ 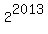 +
+ 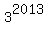 + . . . +
+ . . . +  is divisible by 2013,
i.e. gives zero remainder when is divided by 2013.
is divisible by 2013,
i.e. gives zero remainder when is divided by 2013.
At this point, the problem is solved completely.