SOLUTION: Show that one and only one out of n, n+2, n+4 is divisible by 3, where n is any positive integer

Algebra ->  Real-numbers -> SOLUTION: Show that one and only one out of n, n+2, n+4 is divisible by 3, where n is any positive integer      Log On


   

Question 620766: Show that one and only one out of n, n+2, n+4 is divisible by 3, where n is any positive integer
Answer by ewatrrr(24785) About Me  (Show Source):
You can put this solution on YOUR website!
 

Hi,

Show that one and only one out of n, n+2, n+4 is divisible by 3, where n is any positive integer

Note: number highlight%28n%29must leave a remainder of either 0, 2, or 4 when divided by 3, 

so it can be written as either 3k, 3k+2, or 3k+4 for some k (the quotient). 

If n = 3k: highlight%283k%29, 3k + 2, 3k + 4

If n = 3k+2:  3k+2, 3k + 4, 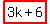highlight%283k%2B6%29

If n = 3k+4:  3k+4, 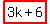highlight%283k%2B6%29, 3k + 8

In each case, one and only one out of n, n+2, n+4 is divisible by 3