SOLUTION: I don't understand the difference between real, rational and complex numbers. I have 5 questions, and I have to figure out if they're real and rational, real and irrational or com

Algebra ->  Real-numbers -> SOLUTION: I don't understand the difference between real, rational and complex numbers. I have 5 questions, and I have to figure out if they're real and rational, real and irrational or com      Log On


   

Question 583451: I don't understand the difference between real, rational and complex numbers. I have 5 questions, and I have to figure out if they're real and rational, real and irrational or complex. Can someone please help me?
1. (567)^1/4
2. (64)^1/3
3. 1/11
4. Π
5. i^2
Answer by KMST(5328) About Me  (Show Source):
You can put this solution on YOUR website!
Rational numbers are ratios of integers (fractions), like 3/5, -1/2, 0, or 8 (0=0/1 and 8=8/1). You can write some of them as "terminating" decimals, and others as repeating decimals, like 1/3= 0.3333... Some rational numbers are integers, and others are what you would call true fractions.
Irrational numbers cannot be expressed as fractions or decimals. You can find approximations that can be written as fractions or decimals, but there are no rules to predict the next decimal digit. They are numbers like pi and sqrt%282%29. They are real, and could be the measurement of something real. For example, sqrt%282%29 is the length of the diagonal of a square with side length 1.
The set of the real numbers is made up of rational numbers and irrational numbers (and nothing else).
Complex numbers are made of an imaginary part plus a real part. They are useful for some applications. The imaginary part is made of the number i=sqrt%28-1%29 multiplied times a real number.
CAUTION:
Teachers like to trick students with expressions like 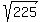sqrt%28225%29, that look like an irrational number, but are a fancy way of expressing a rational number. sqrt%28225%29=15 and 15 is a rational number.
They also give you expressions like i%5E2, that look like an imaginary complex number, but is a fancy way of writing real, rational number -1.
1. %28567%29%5E%281%2F4%29=root%284%2C567%29 is really a real, irrational number
567=3%5E4%2A7, so the number can be simplified, but there will still be a root

2. 64%5E%281%2F3%29=root%283%2C64%29 looks real, irrational, but it is a rational number in disguise"
64%5E%281%2F3%29=%282%5E6%29%5E%281%2F3%29=2%5E%286%2A%281%2F3%29%29=2%5E2=4
3. 1%2F11 is really a fraction, a real, rational number.
4. pi is irrational. You can memorize many digits of its decimal approximation, and win a contest for such an ability, but there is no simple rule to predict the next digit
5. i%5E2 looks imaginary, and you may be tempted to call it a complex number. However,
i%5E2=-1 is really -1 in disguise, so I would call it a real, rational number.
Some may argue that the set of complex numbers includes all real numbers, but I do not think your teacher expects you to call every number a complex number.