|
Question 41656This question is from textbook Elementary and Intermediate Algebra
: What is the difference between a rational number and an irrational number?
This question is from textbook Elementary and Intermediate Algebra
Answer by psbhowmick(878)   (Show Source): (Show Source):
You can put this solution on YOUR website! RATIONAL NUMBER
__________________
Any number which  be expressed in the form be expressed in the form  where 'p' and 'q' (q not equal to 1) are integers mutually prime to each other (this means 'p' and 'q' have no common factors; in other words H.C.F. of 'p' and 'q' is 1) is called a rational number. where 'p' and 'q' (q not equal to 1) are integers mutually prime to each other (this means 'p' and 'q' have no common factors; in other words H.C.F. of 'p' and 'q' is 1) is called a rational number.
e.g. 56, -235.6, 5/7, 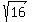 , etc , etc
Note:  . Thus -235.6 can be expressed as a ratio of two integers -1178 and 5 and -1178 and 5 have no factors common between them. . Thus -235.6 can be expressed as a ratio of two integers -1178 and 5 and -1178 and 5 have no factors common between them.
IRRATIONAL NUMBER
____________________
Any number which  be expressed in the form be expressed in the form  where 'p' and 'q' ('q' not equal to 1) are integers mutually prime to each other (this means 'p' and 'q' have no common factors; in other words H.C.F. of 'p' and 'q' is 1) is called a rational number. where 'p' and 'q' ('q' not equal to 1) are integers mutually prime to each other (this means 'p' and 'q' have no common factors; in other words H.C.F. of 'p' and 'q' is 1) is called a rational number.
e.g.  , ,  , ,  , etc , etc
Note: Let us prove that  is an irrational number. is an irrational number.
Let us assume that  is a rational number. is a rational number.
Then it can be expressed as  where 'p' and 'q' are mutually prime integers and 'q' unequal to 1. where 'p' and 'q' are mutually prime integers and 'q' unequal to 1.
Squaring both sides 
or  ______(1) ______(1)
Now, as 'q' is an integer so '5q' is also an integer.
But as 'p' and 'q' has no common factors and 'q' is not equal to 1, so  cannot be an integer. cannot be an integer.
So, there is a contradiction!
Left side of eqn.(1) is an integer but the right side is not.
This cannot be true.
So our very assumption that  must be wrong. must be wrong.
Hence,  is an irrational number. is an irrational number.
|
|
|
| |