SOLUTION: under which operations is the set(1,2,3,....) closed?

If you ADD two numbers in the set, you always get another 
number ii the set. For instance if you ADD 3 + 5, which 
are both in the set, you get 8 which is ALSO in the set.
You CANNOT ADD your way out of the set.

Therefore, it's closed under ADDITION.

If you SUBTRACT two numbers in the set, you DON'T always 
get another number in the set.  For instance if you SUBTRACT 
3 - 5, which are both in the set, you get -2 which is NOT 
in the set.  So you CAN SUBTRACT your way out of the set.

Therefore, it's NOT closed under SUBTRACTION.

If you MULTIPLY two numbers in the set, you always get another 
number in the set.  For instance if you MULTIPLY 3 x 5, which 
are both in the set, you get 15 which is also in the set.  So 
you CANNOT MULTIPLY your way out of the set.

Therefore, it's closed under MULTIPLICATION.

If you DIVIDE two numbers in the set, you DON'T always get 
another number in the set.  For instance if you DIVIDE 3 ÷ 5, 
which are both in the set, you get the fraction  which 
is NOT in the set.  So you CAN DIVIDE your way out of the set.

Therefore, it's NOT closed under DIVISION.

If you EXPONENTIATE two numbers in the set, you always get another 
number in the set.  For instance if you EXPONENTIATE , 
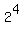which are both in the set, you get 16 which is also in the set.  
So you CANNOT EXPONENTIATE your way out of the set.

Therefore, it's closed under EXPONENTIATION.

So it's CLOSED under ADDITION, MULTIPLICATION, and EXPONENTIATION.

It is NOT CLOSED under SUBTRACTION or DIVISION.

Edwin