1.prove that √3 is irrational
Assume for contradiction that  equals a common fraction
equals a common fraction  reduced to lowest terms.
That is, suppose there are integers p and q
with no common factors other than 1 such that
reduced to lowest terms.
That is, suppose there are integers p and q
with no common factors other than 1 such that
 Square both sides:
Square both sides:
 Multiply both sides by
Multiply both sides by 
 q is either even or odd. Suppose q is even.
Then q^2 is even. Then 3q^2 is even. Therefore
p^2 is even, and therefore p is even. That
contradicts the fact that
q is either even or odd. Suppose q is even.
Then q^2 is even. Then 3q^2 is even. Therefore
p^2 is even, and therefore p is even. That
contradicts the fact that  was reduced
to lowest terms, since if both were even they
would have factor 2 in common.
So we have ruled out q being even, So let's
suppose q is odd. Then q^2 is odd. Therefore
3q^2 is odd. Therefore p^2 is odd. Therefore
p is odd. So there must exist non-negative
integers m and n such that
p = 2n+1 and q = 2m+1. Substituting in
was reduced
to lowest terms, since if both were even they
would have factor 2 in common.
So we have ruled out q being even, So let's
suppose q is odd. Then q^2 is odd. Therefore
3q^2 is odd. Therefore p^2 is odd. Therefore
p is odd. So there must exist non-negative
integers m and n such that
p = 2n+1 and q = 2m+1. Substituting in

 Squaring these out:
Squaring these out:


 Divide through by 2:
Divide through by 2:
 The left side is odd but the
right side is even. That cannot
be, so q is not odd.
q cannot be even or odd, which cannot
be, so
The left side is odd but the
right side is even. That cannot
be, so q is not odd.
q cannot be even or odd, which cannot
be, so  is irrational.
is irrational.
2.prove that if 0 < b < a and n is a positive integer,then
a. 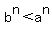
 is given,
therefore
is given,
therefore 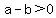 by a factoring theorem
by a factoring theorem
 Since the second parentheses contains only positive terms,
Since the second parentheses contains only positive terms,
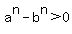 which is the same as
which is the same as 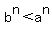
b. 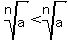 where
where 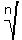 is the positive nth root
is the positive nth root
This follows by replacing  and
and  respectively with
respectively with
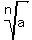 and
and  in part a.
in part a.
c. 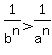
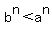 by part a. This is equivalent to:
by part a. This is equivalent to:
 Divide through by the positive number
Divide through by the positive number 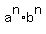
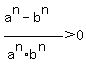
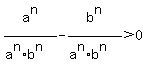
 which is equivalent to
which is equivalent to 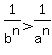 Edwin
Edwin