Question 15389: Let f: R to R be a function. Show that if f is continuous on
[0,infinitive) and uniformly continuous on [a,infinitive) for some
positive real number a, then f is uniformly continuous on [0,infinitive)
(f is uniformly continuous on [0,b] for any b>a).
Thankyou.
Answer by khwang(438)   (Show Source): (Show Source):
You can put this solution on YOUR website! Let f: R to R be a function. Show that if f is continuous on
[0,infinitive) and uniformly continuous on [a,infinitive) for some
positive real number a, then f is uniformly continuous on [0,infinitive)
(f is uniformly continuous on [0,b] for any b>a).
First of all, I wonder why you ask this of calculus or real analysis here.
It seems you should use the theorem that if a function is
continuous on a compact set C(closed and bounded set in R),then
f is continuous on C.
Proof: Now f is continuous on[0,+oo), so as a subset,
f is continuous on [0,a] and thus unif. conti. on [0,a].
Also, we know that f is unif. conti. on [a,+oo).
But, [0,+oo) = [0,a] U [a,+oo) , we conclude that f is unif. conti. on [0,+oo).
More precisely, since f is unif. conti. on [a,+oo)
for any  > 0, there exists > 0, there exists 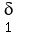 > 0 such that > 0 such that
|x-y|< 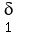 implies {f(x) -f(y)| < implies {f(x) -f(y)| < 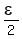
for all x, y in [a,+oo)
And, f is unif. conti. on [0,a]. for the same  , ,
there exists 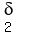 > 0 such that > 0 such that
|x-y|< 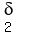 implies |f(x) -f(y)| < implies |f(x) -f(y)| < 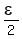
for all x, y in [0,a].
Choose  =min ( =min (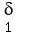 , , 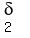 ) the we have ) the we have
|x-y| <  implies |f(x) -f(y)| < implies |f(x) -f(y)| < 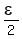
for all x,y in [0,a] (or [a,+oo))
if x is in [0,a] and y is in [a,+oo) we have (Note:a btwn x & y)
|x-y| <  implies |x-a| < implies |x-a| <  and |y-a| < and |y-a| < 
and hence |f(x) - f(y)| <= |f(x) - f(a)| + |f(a) - f(y)|
< 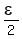 + + 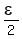 = = 
This shows f is unif. conti.on [0,+oo)
Try to read carefully and draw diagram to understand the details.
Kenny
[Note: you don't have to worry about the interval, [0, b] for any b.
Since [0,b] is compact subset of R. However, f is unif. conti. on [0,b]
for any b > 0 does not imply f is unif. conti. on [0,+oo) as
the example f(x) =  on [0,+oo) shows. on [0,+oo) shows.
|
|
|