SOLUTION: Please help me solve these equations 1) x + y + z = 3 x + 2y - z = 2 x + yz + zx = 3 2) x +yz = 2 y + zx = 2 z + xy = 2

    x + yz = 2,    (1)
    y + zx = 2,    (2)
    z + xy = 2.    (3)

ANSWER.  There are two sets of solutions: (a) (x,y,z) = (1,1,1) and (b) (x,y,z) = (-2,-2,-2).


                                  Solution


First, it is easy to see by inspection that  x = y = z = 1  is the solution.


Next, our goal is to check if there are other solutions.


Let's assume x= 1.  Then equations (1) and (2) take the forms

    1 + yz = 2,    (1')
    y + z  = 2.    (2')


From (2'), express z = 2-y and substitute it into equation (1').  You will get

    1 + y*(2-y) = 2  -->  1 + 2y - y^2 = 2  -->  y^2 - 2y + 1 = 0  -->  (y-1)^2 = 0  -->  y= 1.    (4)


Thus if we assume x= 1, then y= 1  and similarly z= 1.


In the same way, if we assume that any single variable is 1, then we get 
that two other variables are equal to 1, due to equations.


     So, if we are looking for other sets of solutions, 
       where at least one unknown is not equal to 1,
    then no one of the three unknowns in these sets is 1.


    +-----------------------------------------------------+
    |       OK, this step of reasoning is complete.       |
    |    At this point, we start next step of reasoning.  |
    +-----------------------------------------------------+


From equations (1) and (2)

    x + yz = y + zx,

    (x-y) - (xz - yz) = 0,

    (x-y) - z(x-y) = 0,

    (1-z)*(x-y) = 0.       


Since we assume now that  z =/= 1,    we come to  x = y.    (5)


Similarly, from equations (1) and (3) we come to  x = z.    (6)

Similarly, from equations (2) and (3) we come to  y = z.    (7)


    +--------------------------------------------------+
    |     Let before the last attack  w  denotes       |
    |  any of the three equal quantities  x = y = z.   |
    +--------------------------------------------------+


Then equation (1) takes the form

    w + w^2 = 2  -->  w^2 + w - 2 = 0  -->  factoring  (w-1)*(w+2) = 0  -->  w = 1  or  w = -2.


Thus we get these triples  (x,y,z) = (1,1,1)  and  (x,y,z) = (-2,-2,-2),  that we announced as the solutions at the beginning.



Easy check confirms that  (x,y,z) = (-2,-2,-2)  is the second solution set.


There is NO any other solutions.

x + 2y - z = 2
x + yz + zx = 3
2) x +yz = 2
   y + zx = 2
   z + xy = 2

I'll do # 1 for you. Apply the same concept and you should have no problems doing # 2.

       x + y + z = 3______x + y = 3 - z --- eq (i)
                     x + 2y - z = 2 ------- eq (ii)
                    x + yz + xz = 3 ------- eq (iii)

                   2x + 2y + 2z = 6 ----- Multiplying eq (i) by 2 ------ eq (iv)
                     x + 2y - z = 2 ----- eq (ii)
                         x + 3z = 4 ----- Subtracting eq (ii) from (iv) 
                              x = 4 - 3z ----- eq (v)

x + yz + xz = 3____x + (y + x)z = 3 --- eq (iii)
                   x + (3 - z)z = 3 --- Substituting 3 - z for x + y in eq (iii)
                      --- eq (vi)

                  ----- Substituting 4 - 3z for x in eq (vi)
                           

                             z = 1
                              x = 4 - 3z ------ Substituting 1 for z in eq (v)
                              x = 4 - 3(1)
                              x = 4
                              x = 1

                          x + y = 3 - z
                          1 + y = 3 - 1 ------- Substituting 1 for x, and 1 for z in eq (i)
                              y = 2
                              y = 1
                    (x, y, z) = (1, 1, 1)

                             z = - 1
                              x = 4 - 3z ------ eq (v)
                              x = 4 - 3(- 1) -- Substituting - 1 for z in eq (v)
                              x = 4 + 3
                              x = 7

                          x + y = 3 - z
                          7 + y = 3 - - 1 ----- Substituting 7 for x, and - 1 for z in eq (i)
                          7 + y = 4
                              y = 4 - 7
                              y = - 3
                    (x, y, z) = (7, - 3, - 1)

The fact that x, y, and z are purported to have DIFFERENT values would suggest to me that
(x, y, z) = (1, 1, 1) is NOT the solution set, but (x, y, z) = (7, - 3, - 1) instead,
would be the CORRECT solution set!!

I don't think it has to be stated that x, y, and z are different numbers. The fact that they're 
given DIIFERENT variables would automatically mean that they are.

I believe, wholeheartedly, that a note should've been attached to this problem, stating that 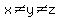.