|
Question 1196050: Which subsets of the real number system are closed under division by a nonzero number?
Found 2 solutions by MathLover1, ikleyn:
Answer by MathLover1(20849)   (Show Source): (Show Source):
You can put this solution on YOUR website!
Non-zero rational number sets is closed under division.
To find : Closed under division from the following sets.
(a) let’s check Natural numbers :
Natural numbers starts from {1, 2, 3, ......., n} numbers.
To find whether natural numbers is closed under division, consider an example :
Assume two values like  and and  . .
Divide  and and  => => 
Resultant 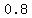 is is  a natural number. a natural number.
So, 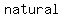 numbers are numbers are   under division. under division.
(b) let’s check Non - Zero integers :
Non-Zero integers which have positive and negative values.
To find whether non-zero integer is closed under division, consider an example :
Assume two non-zero values  and and . .
Divide them, which gives 
Resultant value is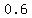 which is which is an an 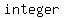 . .
That is, non-zero 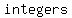 are are   under division under division
(c) let’s check Irrational numbers :
Irrational numbers, a number cannot be represented as fraction.
Eg :  and and 
Divide the values, gives  . .
"  ", which is ", which is  an an 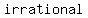 numbers. numbers.
So, 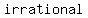 numbers are numbers are   under division. under division.
(d) let’s check Non - Zero rational numbers :
Non zero rational numbers like  , ,  , ,  , ,  and so on. and so on.
To find whether non zero rational numbers is closed under division, consider an example :
Assume two non zero rational numbers  and and 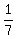 . .
Dividing them we get,  . .
Resultant value is the  numbers. numbers.
Hence, non zero    closed}}} under division. closed}}} under division.
Therefore, non-zero  are are  under under  . .
Answer by ikleyn(52748)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
Which subsets of the real number system are closed under division by a nonzero number?
~~~~~~~~~~~~~~~~
The meaning of your request is really UNCLEAR.
It is written in so mathematically illiterate way, that I should spend half an hour (or more) to explain WHY it is so,
and explain HOW it SHOULD BE, which (time) I definitely do not have to spend it for nothing.
When a person comes with such or similar question, he/she should have some preliminary pre-requisites
and formulate his/her question correctly in the frame of these pre-requisites, in mathematically correct form.
Then he/she may expect to get an adequate answer.
///////////////
Actually, the field of real numbers has INFINITELY MANY sub-fields.
They are sub-fields
- Q (rational numbers),
- 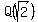 (an extension of Q with irrationality (an extension of Q with irrationality  ),
- ),
-  (an extension of Q with irrationality (an extension of Q with irrationality  ),
- ),
- 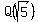 (an extension of Q with irrationality (an extension of Q with irrationality  ),
. . . and infinitely many other sub-fields of the form ),
. . . and infinitely many other sub-fields of the form  , where positive integer number n is not a perfect square, . . .
- , where positive integer number n is not a perfect square, . . .
- 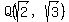 (an extension of Q with irrationalities (an extension of Q with irrationalities  and and  ),
- ),
-  (an extension of Q with irrationalities (an extension of Q with irrationalities  and and  ),
- ),
- 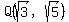 (an extension of Q with irrationalities (an extension of Q with irrationalities  and and  ),
. . . and infinitely many other sub-fields of the form ),
. . . and infinitely many other sub-fields of the form  , where m and n are different non-square positive integer numbers, . . .
- , where m and n are different non-square positive integer numbers, . . .
- 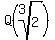 (an extension of Q with irrationality (an extension of Q with irrationality 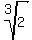 ),
- ),
- 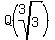 (an extension of Q with irrationality (an extension of Q with irrationality 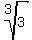 ),
- ),
-  (an extension of Q with irrationality (an extension of Q with irrationality  ),
. . . and infinitely many other sub-fields of the form ),
. . . and infinitely many other sub-fields of the form  , where integer number n is not a perfect cube, . . .
and so on and so on . . . - - - infinitely many others. , where integer number n is not a perfect cube, . . .
and so on and so on . . . - - - infinitely many others.
Each of these sub-fields is a sub-set of real numbers, closed relative addition, subtraction,
multiplication and division by a non-zero elements of these sub-fields.
By the way, when in the school, you learn about getting rid of irrationality  in denominators, in denominators,
you actually learn that the extension  is a field over Q. is a field over Q.
|
|
|
| |