|
Question 1148151: I have to solve the rational inequality and write the answer in interval notation. Could you please provide step by step guidance. I can solve, just want to make sure I have the correct steps.
x^2 - x - 12
____________ > 0
x^2 +x -6
Found 2 solutions by josgarithmetic, ikleyn:
Answer by josgarithmetic(39617)   (Show Source):
You can put this solution on YOUR website!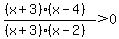 
The critical values for x are -3, 2, and 4.
Test around these values to determine in which intervals the original equation is true.
Note the (x+3)/(x+3) part of the expression will not affect the sign of the whole left-side expression.
Not a complete solution; only guidance.
Answer by ikleyn(52781)  (Show Source):
You can put this solution on YOUR website! .
In your rational function, the numerator is equal to (x-4)*(x+3),
while the denominator is (x-2)*(x+3).
Therefore, this rational function is equal to
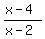 > 0 (1)
everywhere, where the last rational function is defined, except x= -3, where the original rational function is not defined, at all.
Thus our task is to find the solutions of the inequality (1) everywhere, except x= -3.
The function (1) has two critical points x= 4 and x= 2, where the numerator and denominator change their signs.
In the interval x < 2, both the numerator and denominator of the function (1) are negative; so the function (1) is positive.
In the interval 2 < x < 4, the numerator of (1) is negative, while the denominator is positive, so the function (1) is negative.
In the interval x > 4, both the numerator and denominator of (1) are positive, so the function (1) is positive.
Now I am ready to present the
ANSWER : The original function is positive in the intervals
( , ), (-3,2), and ( , ).
Solved.
|
|
|
| |
