|
Question 1084413: What are rational numbers?
Is 7/9 a rational number??
Found 2 solutions by jim_thompson5910, Theo:
Answer by jim_thompson5910(35256)   (Show Source): (Show Source):
You can put this solution on YOUR website!
Rational numbers are numbers of the form x/y where x and y are integers.
The set of integers is {..., -3, -2, -1, 0, 1, 2, 3, ...} basically the set of positive and negative whole numbers including 0.
Keep in mind that because we CANNOT divide by zero, this means that 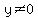 (y can't equal zero). (y can't equal zero).
The value of x can be zero because something like x/y = 0/1 = 0 is possible.
Side Note: The word "ratio" is found in "rational number".
Also, any integer can be expressed as a rational number (eg: 7 = 7/1)
Examples of rational numbers: 1/2, 2/3, 5 (since 5 = 5/1)
--------------------------------------------------------------------------
The fraction 7/9 is a rational number because it is in the form x/y where x = 7 and y = 9.
We don't have to worry about dividing by zero since y is nonzero.
Both 7 and 9 are whole numbers.
Answer by Theo(13342)   (Show Source): (Show Source):
You can put this solution on YOUR website! a rational number is a number that is composed of an integer divided by an integer.
all whole numbers are rational number because they can be viewed as being divided by 1 which is an integer.
7/9 would be a rational number.
rational numbers can be converted to decimals that either have a fixed number of decimal digits or have an unlimited number of decimal digits that are repeating endlessly.
if the number of decimal digits repeat endlessly but do not have a fixed pattern, then the number is not rational.
some examples of rational numbers.
1/2 = .5
1/3 = .3333333................
sqrt(2) is not a rational number.
it is equal to 1.414213562.........
pi is not a rational number.
it is equal to 3.14592654........
e is not a rational number.
it is equal to 2.718281828
while it looks like it has a pattern, when you look at more decimal digits, you will see that the pattern dissolves into random digits with no pattern to them.
9/11 is a rational number.
it is equal to .818181818.........
it's not always easy to tell if a number is rational or not.
in fact, some numbers have never been proven to be irrational or rational.
way back in history, this is a subject that has perplexed mathematicians for hundreds of years. it even got one killed.
here's an excerpt from somee profession in a university in toronto.
History of the Theory of Irrational Numbers
The discovery of irrational numbers is usually attributed to Pythagoras, more specifically to the Pythagorean Hippasus of Metapontum, who produced a (most likely geometrical) proof of the irrationality of the square root of 2. The story goes that Hippasus discovered irrational numbers when trying to represent the square root of 2 as a fraction (proof below). However Pythagoras believed in the absoluteness of numbers, and could not accept the existence of irrational numbers. He could not disprove their existence through logic, but his beliefs would not accept the existence of irrational numbers and so he sentenced Hippasus to death by drowning.
From an encyclopedia entry for "Irrational number" at TheFreeDictionary.com.
if it is a fraction with an integer on top and an integer on bottom, then it is rational.
sometime you have to convert it to integer on top and integer on bottom, such as 1.5/3 is an integer because it can be converted to 3/6 which is equal to 1/3.
most of the time, you can work with a number without knowing if it is rational or not because you're answer is to the nearest 4 decimal digits or nearest 2 decimal digits.
your calculated gives you sqrt(2) that you can work with.
it's not exact, but it is rounded to many decimal digits (about 12 at least), so the impact on any reasonable answer will be minimal to none.
here's some more references.
https://www.mathsisfun.com/rational-numbers.html
https://www.factmonster.com/math/numbers/rational-and-irrational-numbers
https://www.algebra.com/algebra/homework/Surface-area/Surface-area.faq.question.120076.html
|
|
|
| |