Question 1048462: I cant understand how to figure out natural, whole, integer, rational, terminating, repeating, and irrational numbers. I have 5 problems (square root of 14, one third, square root of 2, two thirds, and -10) please help
Answer by MathLover1(20849)   (Show Source): (Show Source):
You can put this solution on YOUR website! recall:
Numbers are classified according to type. The first type of number is the first type you ever learned about:
the counting, or "natural" numbers:
1, 2, 3, 4, 5, 6, ...
the "whole" numbers, which are the natural numbers together with zero:
0, 1, 2, 3, 4, 5, 6, ...
Then come the "integers", which are zero, the natural numbers, and the negatives of the naturals:
..., –6, –5, –4, –3, –2, –1, 0, 1, 2, 3, 4, 5, 6, ...
The next type is the "rational", or fractional, numbers, which are technically regarded as ratios (divisions) of integers. In other words, a fraction is formed by dividing one integer by another integer.
Remember that fractions (also known as rational numbers) can be written as terminating (ending) or repeating decimals (such as 0.5, 0.76, or 0.333333....). On the other hand, all those numbers that can be written as non-repeating, non-terminating decimals are non-rational, so they are called the "irrationals". Examples would be sqrt(2) ("the square root of two") or the number pi ("3.14159...", from geometry). The rationals and the irrationals are two totally separate number types; there is no overlap.
remember:
An integer is a rational number. Since any integer can be formatted as a fraction by putting it over 1, then this is true.
A rational is an integer. Not necessarily; 4/1 is an integer, but 2/3 is not! So this is false.
A number is either a rational or an irrational, but not both. True! In decimal form, a number is either non-terminating and non-repeating (so it's an irrational) or not (so it's a rational); there is no overlap between these two number types!
An irrational number cannot be expressed as a fraction.
Irrational numbers cannot be represented as terminating or repeating decimals.
Irrational numbers are non-terminating, non-repeating decimals.
so, in your case we have:
 ... -> ... -> is an irrational number is an irrational number
 ... -> ... -> is a rational number, repeating decimal is a rational number, repeating decimal
 ...-> ...-> is an irrational number is an irrational number
 = 0.666666666666666666666666666666666666666666666666666666666..-> = 0.666666666666666666666666666666666666666666666666666666666..-> is a rational number,repeating decimal is a rational number,repeating decimal
 -> integer, rational (possibly if written as -> integer, rational (possibly if written as 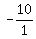 ), real ), real
|
|
|