Question 925986: Write the equation of the quadratic function with roots -9 and and -3 and a vertex at (-6, -1)
Answer by Theo(13342)   (Show Source): (Show Source):
You can put this solution on YOUR website! if the roots are -9 and -3, then the factors are (x+9) * (x+3) = 0
multiply those factors together to get:
x^2 + 12x + 27 = 0
the standard form of the quadratic is ax^2 + b + c = 0
the formula for the vertex of a quadratic equation is x = -b/2a.
in the equation of f(x) = x^2 + 12x + 27
a = 1
b = 12
c = 27
using those values, you would get the x-coordinate of the vertex as:
x = -b/2a = -12/2 = -6.
when x = -6, the value of y = (-6)^2 + 12(-6) + 27 = 36 - 72 + 27 = 63 - 72 = -9.
the value of y is equal to -9.
you need it to be -1.
if you multiply -9 by 1/9, it will be come -1.
so you multiply both sides of the equation of x^2 + 12x + 27 = 0 by 1/9 and you get:
1/9 * (x^2 + 12x + 27) = 1/9 * 0
this results in:
(1/9)*x^2 + (12/9)*x + 27/9 = 0
simplify this to get:
(1/9)x^2 + (4/3)x + 3 = 0
that should be your equation.
now solve for x = -b/2a to get the x-coordinate of the vertex.
x = -b/2a becomes x = (-4/3) / (2/9) which becomes x = (-4/3) * (9/2) which becomes x = -36 / 6 which becomes x = -6.
the x-coordinate of the vertex is still at -6.
now solve for the y-coordinate of the vertex.
f(x) = (1/9)x^2 + (4/3)x + 3 is evaluated at x = -6.
you get f(-6) = (1/9)(36) + (4/3)(-6) + 3 which becomes:
f(-6) = 4 - 8 + 3 which becomes:
f(-6) = -1
now you have the equation where you want it.
you can multiply any equation by a factor and the equation will stretch or shrink along the y-axis without changing the roots, depending on the fraction.
in this case, the original equation of x^2 + 12x + 27 = 0 was shrunk because you multiplied both sides of the equation by 1/9.
the attached graphs will show you what i mean.
here's the equation of x^2 + 12x + 27 as it original was without any multiplication.
when y = 0, the value of x is equal to -3 and -9.
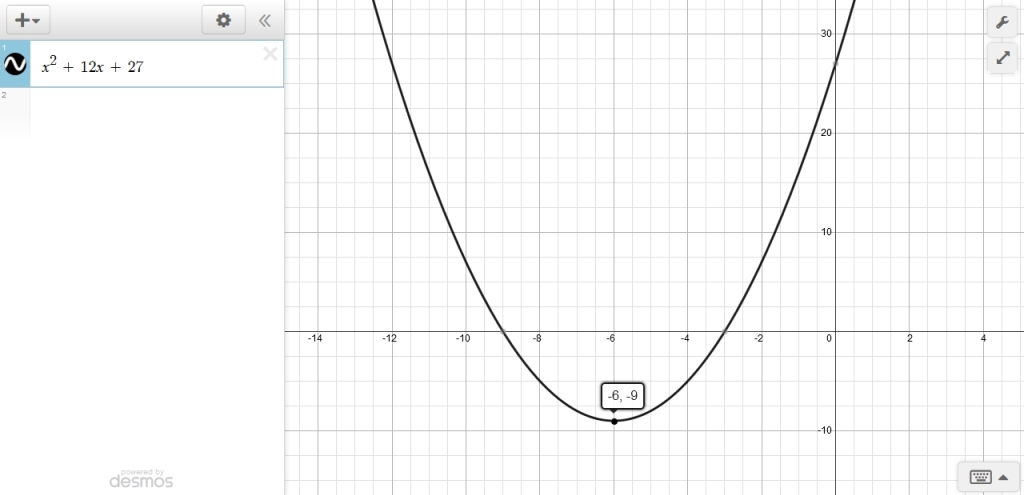
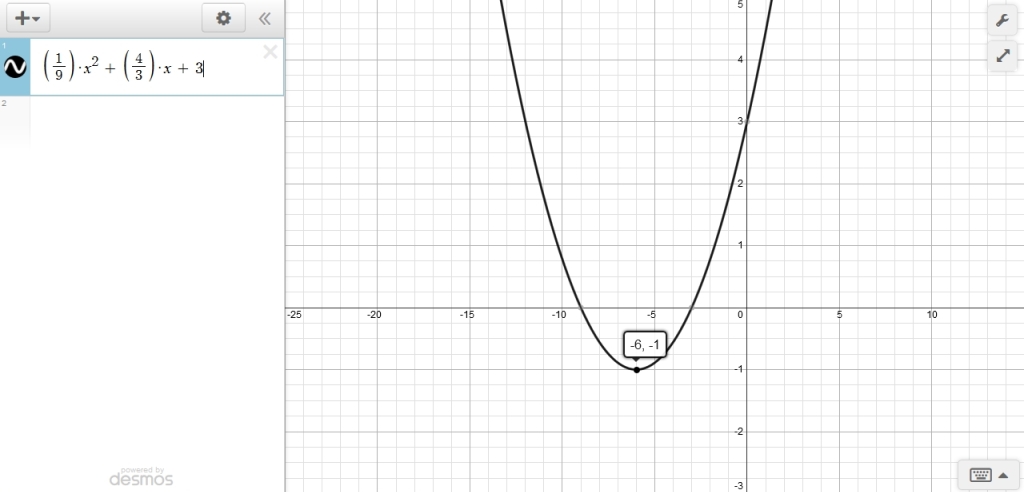
here's the equation of (1/9)x^2 + (4/3)x + 3.
this is the original equation multiplied by (1/9).
the result is that the equation shrinks along the y-axis.
it becomes shorter in both directions from the x-axis.\
the vertex that was at -6,-9 is not as -6,-1.
the roots remain the same.
here's both equations shown together so you can see how the revised graph looks in relationship to the orgiinal graph.
the original graph has a vertex at (-6,-9).
the revised graph has a vertex at (-6,-1).
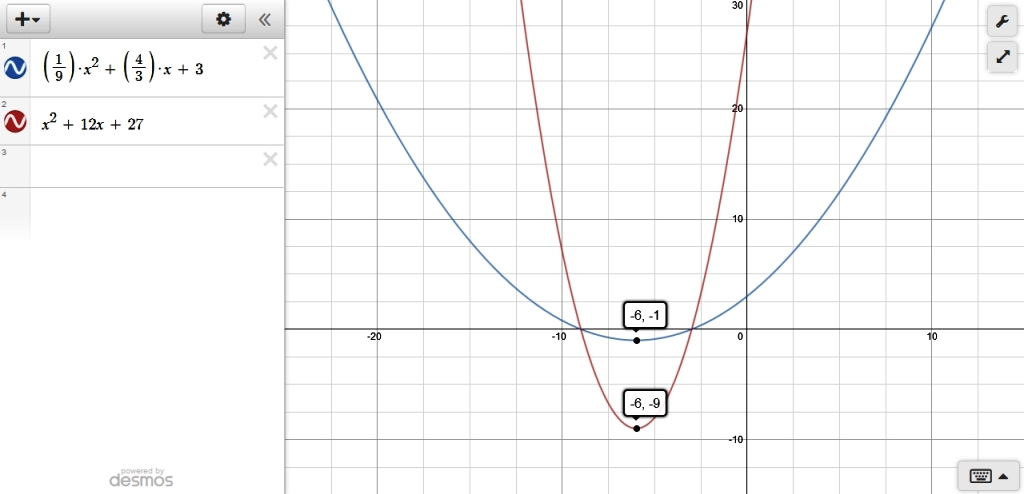
|
|
|