SOLUTION: 1. Solve the quadratic inequality. 2x^2+x-3>0 2. Graph the quadratic inequality. Label vertex, axis, and intercepts. y>4x^2-8x+3 Do you plug it in j

Algebra ->  Quadratic Equations and Parabolas  -> Quadratic Equation Customizable Word Problems -> SOLUTION: 1. Solve the quadratic inequality. 2x^2+x-3>0 2. Graph the quadratic inequality. Label vertex, axis, and intercepts. y>4x^2-8x+3 Do you plug it in j      Log On


   

Question 888045: 1. Solve the quadratic inequality. 2x^2+x-3>0

2. Graph the quadratic inequality. Label vertex, axis, and intercepts.
y>4x^2-8x+3


Do you plug it in just as a normal quadratic problem/formula, or I dont helP
Found 2 solutions by Fombitz, josgarithmetic:
Answer by Fombitz(32388) About Me  (Show Source):
You can put this solution on YOUR website!
1.
You need to find the critical points of the function.
Break up the number line according to those critical points and test the inequality in those new regions.
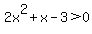
2x%5E2%2Bx-3%3E0+
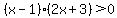
%28x-1%29%282x%2B3%29%3E0
In this case the critical points are,
x=1 and x=-3%2F2
So break up the number line,
1.(-infinity,-3%2F2)
2.(-3%2F2,1)
3.(1,infinity)
Choose a point in each region and test the inequality.
Region 1: x=-2
2%28-2%29%5E2%2B%28-2%29-3%3E0
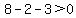
8-2-3%3E0
3%3E0
True
.
.
Region 2: x=0
2%280%29%5E2%2B%280%29-3%3E0
-3%3E0
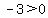
False
.
.
Region 3: x=2,
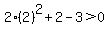
2%282%29%5E2%2B2-3%3E0
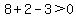
8%2B2-3%3E0
7%3E0
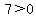
True
.
.
So the solution region is the union of Region 1 and 3.
(-infinity,-3%2F2)U(1,infinity)
.
.
.
2. Convert to vertex form.
y=4x%5E2-8x%2B3
y=4%28x%5E2-2x%29%2B3
y=4%28x%5E2-2x%2B1%29%2B3-4%281%29
y=4%28x-1%29%5E2-1
Vertex (1,-1)
Axis : x=1
X-Intercepts:
4%28x-1%29%5E2-1=0
4%28x-1%29%5E2=1
%28x-1%29%5E2=1%2F4
x-1=0+%2B-+1%2F2
x=1+%2B-+1%2F2
x=1%2F2 and x=3%2F2
Y-intercept:
y=4%280%29%5E2-8%280%29%2B3
y=3
.
.
.
graph%28300%2C300%2C-2%2C4%2C-2%2C4%2C4x%5E2-8x%2B3%29
Choose a point not on the parabola.
(0,0) is convenient.
Test the inequality.
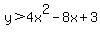
y%3E4x%5E2-8x%2B3+
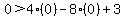
0%3E4%280%29-8%280%29%2B3
0%3E3
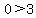
False, so shade the region that doesn't contain (0,0).
graph%28300%2C300%2C-2%2C4%2C-2%2C4%2Cy%3E4x%5E2-8x%2B3%29

Answer by josgarithmetic(39617) About Me  (Show Source):
You can put this solution on YOUR website!
Look for the critical values and test in the intervals around each critical value.

You have 2x%5E2%2Bx-3. Where would this be zero? That tells you the critical values where the sign of the expression changes.

Factorable?
(2x__ 3)(x__ 1), makes 3x and 2x. We want the 2x to be negative signed.
highlight_green%28%282x%2B3%29%28x-1%29=2x%5E2%2Bx-3%29

We have then %282x%2B3%29%28x-1%29=2x%5E2%2Bx-3%3E0.
The critical values for x are at -3/2 and 1.
Pick any one point within each interval and check the sign of the expression.
The intervals are -infinity%3Cx%3C-3%2F2;
-3%2F2%3Cx%3C1;
1%3Cx%3Cinfinity.

ANY point within each interval! Let x=-4, or -5, or -10, no matter. Is the inequality statement true or false?
Let x=-1 or x=0, or whatever in the interval. Inequality true or false?
Let x= something greater than 1.... What happens?

Inequalities do not have a representation in this web system, but maybe you can handle a graph? Cartesian graph, since the inequality is based on a parabola?

graph%28300%2C300%2C-5%2C5%2C-10%2C10%2C2x%5E2%2Bx-3%29

Obviously the given inequality is true for x less than -3/2 or x greater than 1.