Question 862078: How does one evaluate (what is method for) following question...?
"If k is a negative number, which of following equations will have nonreal complex solutions: a) x^2 = 4k, b) x^2=-4k, c) (x+2)^2=-k, d) x^2+k=0 ."
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website! If  is a real number, is a real number,  and and  will be non-negative numbers, so for will be non-negative numbers, so for  , ,
a)  cannot have a real solution. cannot have a real solution.
It has non-real complex solutions.
For the other choices,  makes the squares equal to a positive number makes the squares equal to a positive number
b) 
c) 
d)  <---> <--->
Each one of those equations has two real solutions.
NOTE:
If there was not an obvious square, you would have to make one appear by "completing the square".
Sometimes it is easy as in
 <--> <--> <--> <--> . .
In other cases, you may want to use the work of ancient mathematicians that figured out a general formula to complete those squares.
It turns out that for an equation that can be written as

with any coefficients
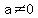 , ,  , and , and  , ,
the square will have the same sign as
 , ,
so if  , ,
the equation 
has non-real complex solutions.
|
|
|