Question 819035: find the quadratic function y=a(x-h)^2 whose graph passes through these points: (9,-12) and (3,0)
Found 2 solutions by TimothyLamb, ikleyn:
Answer by TimothyLamb(4379)   (Show Source): (Show Source):
You can put this solution on YOUR website! ---
This problem cannot be solved as stated.
---
There are 3 unknown variables a, b, and c in the quadratic equation:
f(x) = ax^2 + bx + c
---
Two points are not enough to solve this problem. Please provide a third point.
---
Solve and graph linear equations:
https://sooeet.com/math/linear-equation-solver.php
---
Solve quadratic equations, quadratic formula:
https://sooeet.com/math/quadratic-formula-solver.php
---
Calculate and graph the linear regression of any data set:
https://sooeet.com/math/linear-regression.php
Answer by ikleyn(52760)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
find the quadratic function y = a(x-h)^2 whose graph passes
through these points: (9,-12) and (3,0)
~~~~~~~~~~~~~~~~~~~~
The response by the other tutor is incorrect,
so I came to bring a correct solution.
First use the info, which goes with the point (3,0).
It gives you this equation 0 = a*(3-h)^2,
from which you conclude that h = 3.
Now use the info, which goes with the point (9,-12).
It gives you this equation -12 = a*(9-3)^2, or -12 = 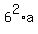 ,
so a = - ,
so a = - = - = - = - = - .
Thus the quadratic function is y = .
Thus the quadratic function is y = 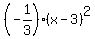 . ANSWER . ANSWER
Solved (correctly).
|
|
|