Question 77604: will someone help me on how to get the particular equation for the quadratic function and will you please show specific step.
The sluggers were up to bat in the bottom of the ninth inning in a game against
the ditchers. Theo Slam was up to bat. As he plugged the ball toward left
field, it rose from 3 to 10 to 50 feet as the horizontal distance from home
plate increased from 0 to 2 to 14 feet. Assume that the vertical distance
varies quadratically with the horizontal distance.
Can someone please help me!!!!!!!!!!!!!!''.
Answer by bucky(2189)   (Show Source): (Show Source):
You can put this solution on YOUR website! Here's a way to get the equation.
.
Presume the equation you are looking for is of the quadratic form:
.

.
where H = the height of the ball and x the distance the ball has traveled horizontally
after contact with the bat. A, B, and C are constants that we will find by using the data
that are given in the problem.
.
For example, we are told that at the point of contact with the bat, x is zero and the ball
is 3 feet above the ground. Put these data into the equation we are developing and you get:
.

.
Notice that the terms containing A and B are both zero and therefore the equation
reduces to 3 = C. Substitute this into the equation and the result is:
.

.
Subtract 3 from both sides so that it becomes a part of the left side:
.

.
We have two more data points. One of them is that when x = 2 ft the height of the ball
is 10 ft. Substitute 10 for H and 2 for x to get:
.

.
The left side terms can be combined and the right side simplified to give:
.

.
Remember this equation. Now let's do the same thing with the final data point. That point
is that when x = 14 ft the height of the ball is 50 ft. Substitute these two values into
the equation to get:
.

.
This simplifies to:
.

.
So now we have two equations involving the two unknowns A and B. They can be solved as
a set. These equations are:
.
 and and

.
Let's solve it by variable elimination. Let's eliminate the terms containing B. Make the
top equation have a B term equal to the corresponding B term in the bottom equation.
Do that by multiplying all the terms in the top equation by 7. When you do the set of
equations becomes:
.
 and and

.
If you subtract the bottom equation from the top one, the B terms cancel each other and
you are left with:
.

.
Solve for A by dividing both sides by -168 and you get:
.

.
You can now solve for B by returning to an equation containing A and B as the two
variables, and substituting  for A. Just to help us, let's go all the way for A. Just to help us, let's go all the way
back to our original equation of:
.

.
We know that  and and  . Substitute those into the equation and you . Substitute those into the equation and you
then have:
.

.
Now let's take one of the data points that has an x value other than zero. It's probably
easier to use x = 2 for a height of 10 ft. When you substitute those values you get:
.

.
Multiply the first term on the right side and you get:
.

.
Subtract 3 from both sides to eliminate the 3 on the right side. This results in:
.

.
By dividing the numerator and denominator by 4, note that the  simplifies simplifies
to 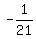 . This makes the equation: . This makes the equation:
.

.
Add 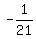 to both sides and you get: to both sides and you get:
.

.
Putting the 7 over a denominator of 21 results in 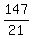 and adding and adding 
changes the left side to:
.

.
Finally, solve for B by dividing both sides of this equation by 2 to get:
.

.
Now putting this into the equation along with  and and  results in: results in:
.

.
That's the equation that will model the path of the ball. Let's try it to see how close
it comes to the actual height of the ball for the three given values of x.
.
When x = 0, as we have seen previously, the two terms containing x go to zero and the
equation reduces to  . .
.
When x = 2, the equation becomes:
.

.
If you run this on a calculator you get:
.

.
That works. As a further check let's try the point where x is 14 ft and see what height
the ball is at at that distance.
.

.
again, using a calculator you find that the individual terms are:
.

.
That works also. The graph of the equation:
.

.
models the path of the ball after the batter hits it. And the graph looks like this:
.

.
From the graph you can see that the top part of the graph is about 254 feet up in the
air, probably higher than a batter can hit it, and the ball goes horizontally about 286
feet before it hits the ground ... not likely to be far enough to be a home run unless
you're talking Little League.
.
Hope this helps you understand the problem and how to develop the equation.
|
|
|