Question 703591: I really appreciate any help with this question:)
A ball is thrown vertically upward with an initial speed of 35m/s. Its height h metres, after t seconds is given by the formula h=-4.9t^2+3.5t.
a)What is the maximum height reached by the ball?
b)How long is the ball in the air?
c)How many seconds is the ball highter than 30m?
I know
a=-4.9
b=35
c+0 I also found the height (which I don't need) using t=-b/2a
Really...really appreciate any help:)!!
Answer by nerdybill(7384)   (Show Source): (Show Source):
You can put this solution on YOUR website! A ball is thrown vertically upward with an initial speed of 35m/s. Its height h metres, after t seconds is given by the formula h=-4.9t^2+35t.
a)What is the maximum height reached by the ball?
because the coefficient associated with the t^2 term is negative, we KNOW it is a parabola that opens downwards. Thus, the VERTEX will be the MAX.
Time t when it reaches max:
t = -b/2a
t = -35/(2*(-4.9))
t = -35/(-9.8)
t = -35/(-9.8)
t = 3.57 seconds
.
Max height, plug t above into equation to find h:
h=-4.9t^2+35t
h=-4.9(3.57)^2+35(3.57)
h= 62.5 metres
.
b)How long is the ball in the air?
set h to zero and find t:
h=-4.9t^2+35t
0=-4.9t^2+35t
0=4.9t^2-35t
0=t(4.9t-35)
t = {0, 35/4.9)
t = {0, 7.14)
throw out the 0 (that's when it started) leaving:
t = 7.14 seconds
.
c)How many seconds is the ball highter than 30m?
set h to 30 and solve for t:
h=-4.9t^2+35t
30=-4.9t^2+35t
0=-4.9t^2+35t-30
0=4.9t^2-35t+30
apply "quadratic equation" to get:
x = {6.15, 1.0}
time higher than 30m:
6.15 - 1.0 = 5.15 seconds
.
Details of quadratic follows:
| Solved by pluggable solver: SOLVE quadratic equation with variable |
Quadratic equation  (in our case (in our case  ) has the following solutons: ) has the following solutons:

For these solutions to exist, the discriminant  should not be a negative number. should not be a negative number.
First, we need to compute the discriminant  : :  . .
Discriminant d=637 is greater than zero. That means that there are two solutions:  . .


Quadratic expression 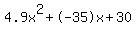 can be factored: can be factored:

Again, the answer is: 6.14682233961713, 0.996034803240008.
Here's your graph:
 |
|
|
|