Question 695021: The volume of a rectangular solid is 540 cubit feet. The width is 3 feet more than the height, and the lenght is 4 more feet than the height. Find the dimensions of the solid.
w=h+3
l=h+4
h= ?
540=(h+3)*(h+4)*h
540=h^3+7h^2+12h
How to resolve ?
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website!  --> --> 
Any rational zero of the polynomial  will be a factor of will be a factor of 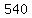 , with a + or a - sign. , with a + or a - sign.

You know we are looking for a positive solution, so I would try + signs first.
The choices for factors are 1,2,3,4,5,6,9,10,12,15,18,20,27,30,36,45,54,60,90,108,135,180,270, and 540.
It is obvious that for positive  values, as values, as  increases, increases, 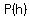 increases. increases.
 and and  , ,
so the solution could be one of the factors in between 1 and 10: 2,3,4,5,6,and 9.
 , ,
so we expect that the solution could be one of the factors between 5 and 10 (either 6 or 9).
 , so , so  is one solution. is one solution.
Is there another solution?
Of course not.
If we make  smaller, the width and length will be smaller, and the volume will have to be smaller. smaller, the width and length will be smaller, and the volume will have to be smaller.
If we make  larger, the width and length will be larger, and the volume will have to be larger. larger, the width and length will be larger, and the volume will have to be larger.
|
|
|