SOLUTION: Write the quadratic function in the form g(x)= a(x-h)^2 + k g(x)= 2x^2 + 12x + 16 Then, give the vertex of its graph. Thanks so much for your help

Algebra ->  Quadratic Equations and Parabolas  -> Quadratic Equation Customizable Word Problems -> SOLUTION: Write the quadratic function in the form g(x)= a(x-h)^2 + k g(x)= 2x^2 + 12x + 16 Then, give the vertex of its graph. Thanks so much for your help       Log On


   

Question 678235: Write the quadratic function in the form g(x)= a(x-h)^2 + k
g(x)= 2x^2 + 12x + 16
Then, give the vertex of its graph.
Thanks so much for your help
Answer by MathLover1(20849) About Me  (Show Source):
You can put this solution on YOUR website!

Solved by pluggable solver: Convert to Vertex Form and Graph
--> 2%2Ax%5E2+%2B+%2812%29%2Ax+%2B+%2816%29
Step 1: Group the first 2 terms together, separating them from the constant term.
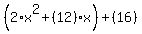
-->%282%2Ax%5E2+%2B+%2812%29%2Ax%29+%2B+%2816%29
Step 2: Factor out leading coefficient, for completing the square to work, the coefficient of x2 must be 1.
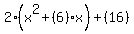
-->2%28x%5E2+%2B+%286%29%2Ax%29+%2B+%2816%29
Step 3: Complete the square, Take half of x coefficient and square it. Notice to keep equation balanced you must add this number and subtract it making the net effect zero.
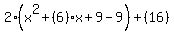
--> 2%28x%5E2+%2B+%286%29%2Ax+%2B+9+-+9%29%2B+%2816%29
--> 2%28%28x%2B%283%29%29%5E2+-+9%29%2B+%2816%29
Step 4: Distribute and add constants.
--> 2%28x%2B%283%29%29%5E2+-18+%2B+16
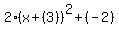
--> 2%28x%2B%283%29%29%5E2+%2B+%28-2%29
Now it is successfully in vertex form and can be easily graphed.
The vertex is at (-3,-2)
The parabola opens up and has a y-intercept at (0, 16)
Here is a graph of this parabola:

graph%28300%2C300%2C-13%2C7%2C+-3%2C+23%2C+2%2Ax%5E2%2B%2812%29%2Ax%2B16%29