SOLUTION: Take quadratic function 3x^2+6x+6 and find coordinates of vertex (h, k). Will it be maximum of the function?

Algebra ->  Quadratic Equations and Parabolas  -> Quadratic Equation Customizable Word Problems -> SOLUTION: Take quadratic function 3x^2+6x+6 and find coordinates of vertex (h, k). Will it be maximum of the function?      Log On


   

Question 668919: Take quadratic function 3x^2+6x+6 and find coordinates of vertex (h, k). Will it be maximum of the function?
Answer by MathLover1(20849) About Me  (Show Source):
You can put this solution on YOUR website!
y=3x%5E2%2B6x%2B6 and find coordinates of vertex (h, k).
3x%5E2%2B6x%2B6=0
if x=0, then y=3%2A0%5E2%2B6%2A0%2B6...=>..y=6
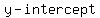
so, y-intercept b=6

if y=0, then 0=3x%5E2%2B6x%2B6...use quadratic formula to solve for x
x+=+%28-b+%2B-+sqrt%28+b%5E2-4%2Aa%2Ac+%29%29%2F%282%2Aa%29+

x+=+%28-6+%2B-+sqrt%28+6%5E2-4%2A3%2A6+%29%29%2F%282%2A3%29+

x+=+%28-6+%2B-+sqrt%28+36-4%2A3%2A6+%29%29%2F6+

x+=+%28-6+%2B-+sqrt%28+36-72+%29%29%2F6+

x+=+%28-6+%2B-+sqrt%28-36+%29%29%2F6+

x+=+%28-6+%2B-+6i%29%2F6+

x+=+-6%2F6+%2B-+6i%2F6+
x+=+-1+%2B-+i+ ....as you can see we have a complex solutions for x which means there is no x-intercepts
so,
x+=+-1+%2B+i+ or x+=+-1+-i+i+
where real part is x=-1 which is our h
so, highlight%28h=-1%29
then, plug it in 3x%5E2%2B6x%2B6=k to find k
3%28-1%29%5E2%2B6%28-1%29%2B6=k
k=3%281%29-6%2B6
highlight%28k=3%29
the vertex is at (-1,3)

+graph%28+600%2C+600%2C+-5%2C+5%2C+-5%2C+10%2C3x%5E2%2B6x%2B6%29+

from the graph you can see that this function has a minimum, and vertex is at (-1,3)