Question 5070: I came across this problem trying to resolve it. I used graphing approach calculating vertices, quadratic and just seem unable to get "reasonable" or real solution.
Q. If the bus ticket is 1.60 the average number of riders is 2000. The bus company considers raising the ticket, but on every 0.10 increase they loose 100 riders. What should the bus company charge to maximize their profits.
So far I have:
(2000-100x)(1.60+0.10x)=0
y=-10x^2+40x+3200
Thanks a bunch, Mike
Answer by longjonsilver(2297)   (Show Source):
You can put this solution on YOUR website! Look at the first few situations...
1.6*2000 --> 3200
1.7*1900 --> 3230
1.8*1800 --> 3240
1.9*1700 --> 3230
This gives you the answer of 1.80 as the amount to charge to maximum their revenue. How do to this algebraically?
Well, looking at the above sequence, we have in general:
(1.6+0.1x)*(2000-100x), where x is just a number, 0, 1, 2, 3, 4 etc
so revenue, r = (1.6+0.1x)(2000-100x). This expands to be
r =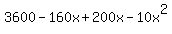 
r =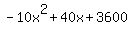 
r =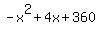 
Differentiate, giving dr/dx = -2x + 4.
So when is this equal to zero? ie when does the curve "turn"?
-2x+4 = 0
--> 2x = 4
so x = 2 but is it a max or min?
 : negative --> therefore max.
So, the maximum occurs when x = 2, ie should charge 1.60+2(0.1) = 1.80, which agrees with our common sense approach we did first.
jon.
|
|
|
