SOLUTION: find the value of k for which the line y=x+k is a tangent to the curve y to the power of 2=5x+10.

I cannot tell whether you are taking calculus or are still
in algebra.  So I'll do it both ways.

--------------------------------------------------------

If you are taking algebra, this is the way to approach it:

Here is the graph of y² = 5x + 10



Here is a graph of the line y = x + 2.5 where k=2.5



As you can see that line is not quite tangent to the parabola, 
because it intersects the parabola in two places.  So k=2.5 is
not quite large enough.

Here is a graph of the line y = x + 4 where k = 4



And as you see that graph doesn't intersect the parabola at all.
So k=4 is too large.  

We want to find the exact value of k, so that the line whose equation
is y = x + k only has one point of intersection with the graph.  So we
solve the system of equations:

y² = 5x + 10
y = x + k

and find k so that there is just 1 solution, not 2 or 1.
So we substitute (x + k) for x in the first equation:

               (x + k)² = 5x + 10
          x² + 2kx + k² = 5x + 10
x² + 2kx - 5x + k² - 10 = 0
x² + (2k-5)x + (k²-10) = 0

That will have one solution when the discriminant b²-4ac = 0

b²-4ac = (2k-5)² - 4(1)(k²-10)
       = 4k²-20k+25-4(k²-10)
       = 4k²-20k+25-4k²+ 40
       = -20k+65

So we set that = 0

     20k+65=  0
         2k=-65
          k=
          k=

That's the answer.  Now as a graphical check, 
when we graph y = x -  we get:



We see that the line y = x -  is exactly tangent to
the graph of y² = 5x + 10

So we are satisfied with our answer k = 

--------------------------------

Now if you are taking calculus, you will find the derivatives of
both the line and the parabola and find where they are equal:

The derivative of 

y = x + k   is


The derivative of 

y² = 5x + 10
2y = 5
=

We set the derivatives equal




That is the y-coordinate of the point of tangency.

Now we substitute that in 

y² = 5x + 10
()² = 5x + 10
 = 5x + 10
25 = 20x + 40
-15 = 20x
 = x
 = x

That is the x-coordinate of the point of tangency.
So the point of tangency is (, )

Substituting that in the equation of the line:

y = x + k
 = (((-3/4}}} + k
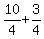 = k
 = k
 = k

Either way we get k = 

Edwin