Question 482758: -10 and -7
The Quadratic Equation is ?= 0
Answer by bucky(2189)   (Show Source): (Show Source):
You can put this solution on YOUR website! From your problem, you know that the roots are:
.
 and and 
.
That means that the factors of the quadratic equation are:
.
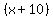 and and 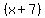
.
When you multiply these two factors together (use the FOIL process ... multiply First terms in the two sets of parentheses, then Outside terms, then Inside terms, and finally Last terms) you get the quadratic form:
.

.
and this simplifies to:
.
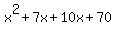
.
which by collecting the two terms containing the x becomes:
.
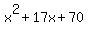
.
and therefore the quadratic equation is:
.

.
To show you why this works, let's do the problem in reverse. Start with the answer we have, namely:
.

.
Solve this equation by factoring:
.

.
And here comes the critical part ... this equation will be true if one of the factors equals zero. This is because if a factor is zero, in the left side of this equation zero times anything equals zero, and the left side therefore will equal the zero on the right side. So, we can say the equation is true if either:
.
 or if or if 
.
For the first factor to equal zero, you can see that x must equal -10 and for the second factor to equal zero, you can see that x must equal -7. These are the two roots that you were given in the problem, so we know that our equation:
.

.
is the correct solution to this problem.
.
Hope this helps your understanding of the problem and its solution.
|
|
|